Recent changes
Table of Contents
BACKGROUND:
First Electronic Computer (speed for scientific problems)
|
There were about six serious efforts in the ten year period (1935-1945) to use machinery
to aid in solving scientific oriented computing.
Here is a Mini History of the efforts.
The above mini-history history does not include commercial data processing problems, such as inventory, billing, payroll, ..., which were being handled by
a group of companies, including the famous International Business Machines ( IBM ).
- - - - - - - - - - - - - - - - - - -
There is a viable claim that the "First Electronic Computer" (as in computing machine)
- was conceived and designed by John V. Atanasoff
- and constructed by Clifford Berry
- at and funded by Iowa State College.
- It also used the first "dynamic memory" - the principles used in your computer today, invented by Atanasoff.
- First use of binary arithmetic, used in your computer today
- First actually constructed parallel machine. (Babbage designed parallel into
his second design for his polynomial evaluator (difference engine), but did not complete construction.
- First SIMD ( Single Instruction Multiple Data ) machine. The pivot values determine whether add, subtract, shift right -
will be performed on all data elements of the two vectors in the ABC memory drums.
|
First Scientific Problem on Electronic Computer
|
The
"ABC" was an equation solving machine, constructed to find the variables of
up to 29 simultaneous equations, and was successfully tested in 1942.
It could not run Windows ;-)) nor do most other current computery things
such as play games.
However - it was a "giant leap" in the quest for
solving simultaneous linear equations.
Here is a simultaneous linear equation
|
|
| x
| +
| 2y
| +
| 3z
| =
| 39
| x
| +
| 3y
| +
| 2z
| =
| 34
| 3x
| +
| 2y
| +
| z
| =
| 26
| | |
|
|
Many high school students learn to "solve" this size problem,
and by extension, larger number of equations with larger number of unknowns.
BUT
It quickly becomes apparent that solving larger numbers of equations and unknows
becomes very time consuming and error prone :-((
|
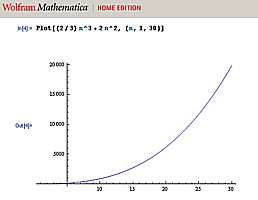
Level of Computational Effort in solving Simultaneous Equations
John Gustafson
gives this approximation for the number of operations to solve
n equations with n unknowns.
"For people who use operation counts to measure complexity, the solution of a linear system with n unknowns is
(2/3) n^3 + 2 n^2
where a multiply and an add are each counted as one floating-point operation. There are also order n terms, usually ignored. You cannot avoid doing n divides somewhere along the way, for example."
|
number of
variables
(equations)
| Approx.
operation
counts
| 3
| 36
| 5
| 133
| 10
| 866
| 20
| 6,133
| 29
| 17,942
| | | | | |
|
|
 click to enlarge
click to enlarge
|
Many of us have enough trouble doing thirty six 5 digit multiplies (practical data precision) and adds with out a blunder :-((
|
More information on the First Electronic Computer
- An ABC reconstruction has been completed at Iowa State University,
- -
JVA (John V. Atanasoff) web page
- -
re-construction pictures
- - LARGE formal picture of re-construction.
- A very useful book, mentioned above,
The First Electronic Computer: The Atanasoff Story
by Burks and Burks, is available. The first 70 pages and an appendix
are very useful to techies.
- Another fascinating book is
Atanosoff, Forgotten Father of the Computer with much human interest.
- Another view of "first"
ENIAC: The Triumphs and Tragedies of the World's First Computer
- Useful/Interesting web sites etc.
- -
Oral history - J. V. Atanasoff - Smithsonian Institution
- -
Making first computer come to life again
- -
Current ABC Reconstruction Team
- -
Reconstruction of the Atanasoff-Berry Computer by Dr. John Gustafson
- - - - paper
by Dr. John Gustafson
- Contacts:
John V. Atanasoff Jr., Dr. Carl Chang (ISU prof),
Dr. John Gustafson (Reconstruction Project Mgr), Charles Shorb, Gary Sleege, Guy G Helmer,
Laurel Tweed - current program coordinator, Alice R Burks - co-author of "
The First Electronic Computer: The Atanasoff Story"
- A list of interesting pictures - at Iowa State web site
- - ABC Current Events
- - Current ABC Reconstruction Team
- There is an amazing amount of heat between Atanasoff "supporters" and ENIAC "supporters".
Reminds me of the computer operating system wars, or computer language wars -
- Now that I've offended both sides,
I'm just here to learn a little and have a good time.
- As Atanasoff is quoted,
- "There is more than enough credit for all."
- I have had trouble finding practical uses/needs for a machine which can solve simultaneous equations
for more than 5 unknows, much less 29 unknowns. Atanasoff in his
oral history
mentions "complex spectra work". Searching for other uses yielded these.
|
Documentation Needed
- ABC Machine Operator's Manual - likely never written for the original machine - WWII called
My (Ed Thelen's) start of an 'Operator's Manual'
Charles Shorb's start of User Manual / Guide for the ABC in PDF.
-
- Maintenance and Trouble Shooting Manual - likely never written for original machine - WWII called
- I probably won't write one either ;-))
- A place for documents and comments by the reconstructors ??
- ?John Gustafson? mentioned using repeating ( ?5x5? ) problems to assure
rather complete testing
- ?Voltage margin testing
- Acceptance Tests - likely never written for the original machine - WWII called
- A complete simulation should pass these
- Input test cases, and expected results for each,
- probably no discussion of results/hour, uptime, ... ;-))
- John Gustafson suggests simulating the worrysome data punching errors
to estimating the largest practical array size -
|
Simulation Goal:
- Use a PC and open source code to emulate and display most of the
functionality of the ABC [ Computer }
- Except the card "punch", card reader, and decimal conversion machinery
- - I/O is visible as decimal and binary.
- - Intermediate results, equation coefficients, are stored in PC memory
not physical media.
- Making the internal states and operations visible
- Atanasoff used a variation of Gaussian Elimination, using kind of a
"microcoded" division to form the correct ratios to permit coefficient elimination.
(Determine the values of the variables.)
- Showing the progress of the elimination of the variables in
the succeeding stored equations.
- I am using FREEBASIC
with the "FBIDE" developer's interface, because I can paint an arbitrary pixel with an
arbitrary color !! You would be surprised how few languages
permit you do that. It gets compiled to machine code and runs fast :-))
- Shows the Gaussian selection of equation pairs
to load into the ABC, and a pivot point, for Gaussian elimination.
You don't have to be a matrix whiz :-))
- This provides a better reconstruction of operator activities.
(The actual equation input, processing, and output are rather automatic after selection.)
- Provide a section "Why are people interested in solving
simultaneous equations?" Like why bother?
- Provide the code and show the source of the compiler to help assure
potential users that there are no virus present. The user can examine,
compile, and run the source code.
- Posssibly provide a JAVASCRIPT version for safe running on your PC -
- Just plain have fun ;-))
|
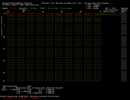
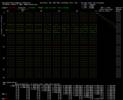
Graphical User's Interface
- (Monitor must be at least 1280x1024, Tested on a PC running Windows XP)
- PLEASE NOTE & REMEMBER: click mouse on "EXIT"
(middle of top line) or type "q" to quit the program.
ABC-0V2-Sim10-03-21.exe - .exe file for images below - click to download and run (on a PC) - 106 KBytes
ABC-0V2-Sim10-03-21.bas - source file for images below - 47 KBytes
|
This Graphical User Interface is at Alpha 1.0 release, Bit fields rotated 90 degrees from 0.1 release, card reading/writing vectors added.
Images of monitor are about 150 KBytes
| 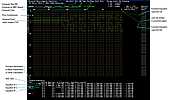
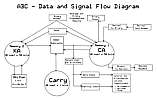
| Atanasoff used terminology similar to the desk calculators of the era because current terminology
hadn't been developed yet - although he was the ?first? to use the now universal word "memory".
- "Keyboard" (KA) is the equation being compared in this cycle, shifted in processing
- "Counter" (CA) is the equation being modified for the elimination, modified
- Carries, being of some interest, are also painted
|
-
Movies of the simulated ABC doing 15 seconds of a 9 unknown set of equations
- -
ABC Speed, 1 rotation per second - .wmv file, 1.5 MBytes
- -
Your Computer Speed, fast speed - .wmv file, 1.5 MBytes
|
- I'm trying to make the display sexy, attractive, sparkle, ...
"If I look at this, I can drive my convertible on the beach,
and the girls will flock about"
- you know those ads ;-))
- As best I can figure, most folks know of simultaneous equations
only as a topic to torment high school "math" students.
- If folks have some clue why solving equations of more than say
three unknowns, they might give a hoot.
Solving for just one unknown is usually puzzling enough !! ;-))
-
Why would some guy in Iowa ( or anywhere for that matter )
want to solve for up to 29 unknowns?
- So your GPS receiver solves 4 simultaneous equations each second, GPS is magic anyway -
- Your comments on the above are solicited - Send e-mail
or (510) 742-1146
|
|
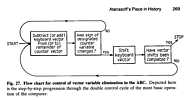
Pages from the Burks & Burks book - the best published technical reference
Six vital pages from
"The First Electronic Computer: The Atanasoff Story"
(above)
are being made available courtesy of Alice R. Burks - each about 150 K Bytes
|
|
|
From the school of hard knocks
- The algorithm on page 269 (above) has been simplified too much -
There needs to be a check for the pivot CA being zero after the arithmetic, if zero, stop, go to next pivot.
- Many simple examples of integer simultaneous equations with known integer solutions
give wildly incorrect results with Atanosoff's ratioing - unless scaled up by factors of say 10000.
This link provides examples with exact and non-exact answers as run under
Atanosoff rules.
- A further problem, somewhat alleviated by more scaling, is where the coefficients differ by several orders of magnitude.
a small coefficient not on the pivot can get shifted right to become zero very early in the ratioing cycle -
introducing further inaccuracies. It is easy to imagine that Atanosoff selected the large fixed point capability - 50 binary bits or
about 15 decimal places to help fight the above problems.
- You may begin to appreciate floating point computations which (usually) eliminate the scaling problems noted above. We are so spoiled,
and can work so much faster, and confidently, with much less concern about various overflows and underflows. I am so thankful -
|