Go Forward, Go Back, Go to Table of Contents, Go to On Line Documents, Go to Go to Antique Computer home page


Reckoners, Bell Labs, page 0073



4
Number, Please
Computers at Bell Labs



.
The Bell Telephone Laboratories general-purpose relay computer is probably the best mechanical brain made up to the end of 1947 . . . .
-Edmund Berkeley, 1949

A telephone network does two things. First, it transmits voices from one person's phone to another's. Second, it allows a person to select the caller he or she wishes to speak with-by letting the caller "dial" a phone connection. Obviously the first is the essence of what a telephone is-that was what Alexander Graham Bell invented in 1875. But the second is just as important to the telephone system as it is used today. The two functions are basically different: one is concerned with continuously varying signals generated by the human voice, the other is a cascading of yes-or-no switches that establishes a path between two subscribers. One is an analog process, the other digital.

Between 1937 and 1946 engineers and scientists at Bell Telephone Laboratories built a number of digital relay computers, among the first working programmable machines anywhere. Their experience with the technology of switching-that second aspect of telephony-was the basis for Bell's entry into digital computing. But the first aspect-the transmission of analog voice signals-played a role too, as we shall see. The invention of the computer at Bell Laboratories, like its invention elsewhere, resulted from a convergence of technical skill, social need, and talent. Those preconditions were there by the mid-1930's. It remained for one of Bell's employees, Dr. George Stibitz, to serve as the catalyst to bring them together.
Reckoners, Bell Labs, page 0074

BACKGROUND: BELL LABORATORIES

A telephone codes information (the sound of the human voice) into electrical signals, transmits those signals over wires, and decodes them into sound at the other end. The engineers who worked on this form of "data processing" (of course they did not use that term) in the early days had little theory to guide them. For short distances it was easy enough to send voice signals; indeed Alexander Graham Bell's original circuit was terribly inefficient from a modern standpoint, yet it worked well enough to launch the industry.

But for long distances the problem of keeping the signal intelligible became acute. The first circuits were limited to a range of a few miles before the signal faded out.

With that restriction on the telephone's use, it did not compete with Western Union, the dominant telecommunications company of the late 19th century. Western Union handled digital information (dots and dashes) that could be regenerated by "repeaters" along a line, thereby allowing coast-to-coast communication. But telephone signals vary continuously over a large spectrum. As they lose their strength they cannot be regenerated by a repeater. They have to be amplified instead.

So the telephone coexisted with the telegraph in its first few decades of existence. Its personal service, using the human voice and not a code, suited it well for local urban traffic. Western Union's telegraph handled long-distance messages.

The Bell company was not satisfied with that state of affairs. It introduced a number of improvements to increase the distances over which telephone signals could be sent: the two-wire circuit in the 1880's, the "loading coil" after 1900, and others. But it was the adoption and perfection of the vacuum-tube amplifier after 1912 that finally made amplification, and hence transcontinental service, practical. (The first transcontinental call was made in July, 1914.)1 Establishing reliable (and cheap) long distance service launched Bell into a period of steady growth until it had all but relegated the telegraph to a back corner of the telecommunications world.

So the success of the Bell System depended on its ability to transmit and amplify telephone messages over long distances. That success in turn came from recognizing the potential value of the "audion" vacuum tube (invented by Lee DeForest in 1906) and improving it to the point where it would function as a reliable amplifier. DeForest had not really understood the fundamentals of his own invention; a strong research effort by Bell Telephone revealed the nature of the tube's function-and turned it into a practical device.

It was for that purpose that a laboratory for basic research was established in 1911, as a branch of Western Electric, Bell's manufacturing company.2 In 1925 the lab was incorporated as the Bell Telephone Laboratories, and given charge of basic research for the Bell System, which by then had become a powerful monopoly under the leadership of Theodore N. Vail. Thus began an institution that has become synonymous with fundamental and exciting research at the frontiers of physics, chemistry, and other branches of modern science.


Reckoners, Bell Labs, page 0075

Research on the physical problems of long-distance telephony was what started Bell Laboratories, but by the 1930's it was busy with that other aspect of telephony, switching, as well. The earliest networks used human operators to route a caller to the desired callee, and indeed there are places in rural America where calls are still placed that way.3 But from the beginning of personal phone service there was an effort to automate the call-selection process. Many historical accounts mention that an undertaker named Almon B. Strowger invented the automatic rotary dial in 1891 to prevent operators from being bribed to divert business to his competitors.4 Whether or not that story is accurate, it does show that the telephone system was closely linked to automatic switching from the start. After 1921 the dial began replacing operators in significant numbers. It is still in wide use today, although the push-button "dial" is now replacing it.

The engineers who designed the first switching circuits were, in effect, using electromagnetic relays to implement "logical networks," although they did not consider their work in those abstract terms. Some of the circuits they developed were quite sophisticated: for example, if all the major trunk lines between two cities were busy, a call would be automatically rerouted through another line, perhaps through a third city, all automatically. While the switching equipment was setting up this path, other banks of relays would store the dialed number and then retrieve it when the call was ready to go through. These two functions- automatic selection of a circuit depending on the present condition of the net-work, and temporary storage and retrieval of numbers-are of course also central to the operation of computers.5

In retrospect it seems inevitable that someone at Bell Laboratories would adapt that switching equipment to function as a digital computer. But for what purpose? The switching circuits were already doing their job well; why adapt them to function as a general-purpose computer unless there was an obvious need for one? The Laboratories were committed to basic research in a variety of fields, and in 1925 that was something remarkable for an industrial laboratory in America. Nevertheless they were always mindful of the original purpose for which the labs were set up: in Theodore N. Vail's memorable phrase, "one system, one policy, and universal service."6 Bell's engineers would build a digital computer only if they believed it would further those goals.

By the 1930's they saw the possibility of using relay circuits to perform ordinary arithmetic, as commonly performed with mechanical calculators.7 Telephone switching circuits did not perform arithmetic in the ordinary sense, but they did convert numbers from their dialed code of pulses into other pulses that actually did the switching. It would have been an easy matter to have those conversions mimic the familiar laws of addition and subtraction of numbers. But there was no point in building a calculator out of relays, since existing mechanical calculators already worked well, and there was no reason to believe that relay calculators would be better--or cheaper. But a calculator that took advantage of the relay's ability to perform logical switching as well-something mechanical calculators could not do-would be justified, if there was a mathematical problem demanding that capability.

As it turned out, such a problem was being faced by the other division of Bell Labs-the division that worked with long-distance transmission of analog voice signals. Dr. George Stibitz, a research mathematician at the Labs, was the pivotal figure who matched the needs of that group with the capabilities known to the switching engineers. The result of this marriage was the Complex Number Computer, completed in 1939, which though not a programmable general-purpose computer, nonetheless inaugurated Bell's involvement in the computing field.
Reckoners, Bell Labs, page 0076

COMPLEX NUMBERS

The Complex Number Computer performed the four ordinary operations of arithmetic, but on complex rather than simple numbers. Complex numbers were used in the design of filters and amplifiers for long-distance telephone lines. The function of those devices was to maintain the strength of the desired voice signal, while at the same time keeping the level of unwanted signals (for example "noise") low. But the engineers had to be concerned with more than just the amplitudes of the signal and noise. They were also concerned with the "phase" of the signal-the relationship of the ever-varying voice signal with time. Filters and amplifiers introduced time-delays into the circuit, and unless those delays were accounted for, the resulting signal might be reduced rather than increased in strength. (One familiar example of phase effects is found in home stereo Systems. The two loudspeakers, which deliver the left and right components of the reproduced sound, must be in phase with each other. If the phase is incorrect, the sound from one speaker will cancel out the sound from the other, regardless of the power of the amplifier. A similar situation occurs in telephone circuits.)

Engineers found that they had to represent a signal by a pair of numbers, one corresponding to its amplitude, the other to its phase, in any mathematical model of the physical processes they were dealing with. The key to the success of this method was that by following certain rules for the addition, subtraction, multiplication, and division of these pairs of numbers, the mathematical results corresponded closely to what happened when electrical signals combined with one another in a circuit.

Long before the first telephone line had been built, mathematicians had devised rules for working with pairs of numbers that arose in the solutions of certain algebraic equations. In devising those rules for "complex numbers," they wanted something useful for the work they were doing, but they were also concerned with making those rules logically consistent. That is, the rules for complex arithmetic were an extension of, and did not contradict, those of ordinary simple arithmetic.8

Historically the study of complex numbers arose from the study of quadratic equations, in which certain solutions could only be gotten by taking the square root of a negative number. Thus the "imaginary" quantity i, the square route of -1, was introduced. The second number of the pair that makes up a complex number was thought of as being multiplied by this quantity.
Reckoners, Bell Labs, page 0077

For electrical engineers it did not matter how this theory arose, or even what i stood for, for that matter. (They did not use the letter i either, since it might be confused with the symbol for electrical current, so they used j instead.) What did matter was that the rules for manipulating those numbers were consistent with ordinary arithmetic, and that they were useful for the analysis of electrical signals. The history of mathematics has many other examples of a theory finding unexpected applications that its creators never anticipated. (Probably the most famous example was Apollonius's study of the conic sections, written in the third century B.C.: it was lost to the West for centuries, then in a breathtaking leap-twenty centuries later-Johannes Kepler used those curves to explain the motions of the planets around the sun.)

The mathematicians who developed complex arithmetic lived too early to see its application to telephone circuits, but at least one of them, Carl Friedrich Gauss, would not have been surprised-he built Europe's first telegraph in 1833, connecting his house with his laboratory at Gottingen!

Incidentally, the use of complex arithmetic as a tool for the analysis of electrical circuits was pioneered by Charles P. Steinmetz, an immigrant to America who worked at the General Electric Laboratories on power distribution. Years later the analysis of telephone signals yielded to that same theory (despite their being more complicated than power currents).9

The engineer used a pair of numbers to represent the amplitude and phase of a signal, not the real and imaginary parts of the solution to an equation. When two signals were combined their addition corresponded to the addition of the two complex numbers:

(a, b) + (c, d) = (a + c, b + d)

Similarly for subtraction:

(a, b) - (c, d) = (a - c, b - d)

In physical terms, when two signals are added to each other, their amplitudes and phases are added separately.

Multiplication and division are less easy to visualize, but they represent what happens to signals when they pass through various stages of amplification and filtering. In establishing a coast-to-coast telephone line in the 1930's, Bell Labs was engaged in the design of filters and amplifying circuits, whose operation introduced phase delays into a signal. The analysis of those circuits required complex multiplication and division.10

The rules for multiplication and division are:

(a, b) x (c, d) = (ac-bd, ad + bc)
(a,b) / (c,d) = [(ac+bd)/(c2+d2), (bc-ad)/(c2+d2)]

Note that in each of the above rules, when the second (phase) term is zero, the rules reduce to those of ordinary arithmetic. Complex arithmetic extends the range of arithmetic; it does not replace it.
Reckoners, Bell Labs, page 0078

Bell Labs employed a staff of about five to ten women who worked full-time computing products and quotients of complex numbers. (Addition and subtraction were presumably simple enough for the engineers to do for themselves.) For the arithmetic they used electromechanical desk calculating machines.

We see from the above formulas that multiplication of complex numbers requires four simple multiplications, one simple subtraction, and one simple addition. Complex division requires six multiplications, two additions, one subtraction, and two divisions of ordinary numbers. In each case several intermediate results appear-they have to be written down and retrieved later on.

George Stibitz saw that the switching circuits the relay engineers were working on in one part of the Labs could compute complex products for the voice circuit engineers in another part of the Labs. That relays could do arithmetic was already known; Stibitz had constructed a simple adder out of binary relays as early as 1937. That alone meant little. But if the relays could also perform the sequencing and temporary storage that complex arithmetic demanded (and which ordinary calculators could not do), then such a calculator would have a practical use. He later remarked that as a research mathematician he was familiar with complex numbers but not with relay circuits. On the other hand relay engineers were probably less familiar with complex numbers since these did not arise in their work very often.11 That may be an exaggeration, but remember that switching circuits were designed in a trial-and-error fashion; there was little theory for them in 1935. Complex arithmetic was a child of pure mathematics-the nomenclature "complex," "imaginary," and "square root of minus one" does not help make this tool more accessible to someone not mathematically sophisticated. In any case, Stibitz made the connection.

GEORGE R. STIBITZ

George Robert Stibitz was born on April 20, 1904, in York, Pennsylvania, and spent his childhood in Dayton, Ohio, where his father was a professor of theology at a local college. He showed a talent for engineering and science at an early age, and so he attended an experimental high school set up in Dayton by Charles Kettering, the inventor of the automobile starting system.12 He attended Denison University in Granville, Ohio, receiving a B.Phil., and then went on to Union College in Schenectady, New York, where he received an M.S. in 1927. Schenectady was of course the home of General Electric's research laboratory (cf. Steinmetz's work with complex numbers), and for a while Stibitz worked there. He returned to school, however, and received a Ph.D. in mathematical physics from Cornell in 1930, after which he went to New York City to work for Bell Labs. His doctoral dissertation concerned the study of the vibrations of nonplanar membranes.13


Reckoners, Bell Labs, page 0079

From 1930 to 1941 Stibitz worked for Bell Laboratories-that was when he pioneered the use of relays for automatic computation. During World War Two he was a member of the National Defense Research Committee (NDRC), where he worked on computing and other projects. At the end of the war he moved to northern New England, where he has lived ever since. He worked as a private consultant in Burlington, Vermont, and since 1964 he has been a professor of physiology at the Dartmouth Medical School in Hanover, New Hampshire. He is still active there in projects involving the use of computers in medicine.

In the fall of 1937 Stibitz was working with a group of mathematicians who were designing relay switching equipment. He took a few relays home one evening and assembled a device that could add two binary digits as indicated by lamps which glowed for the digit 1 and were dark for the digit 0. (In later years the computer world would take notice of these milestones, and so just as the mechanical devices Zuse built in his parents' flat would later take on the name "V1," and then "Z1," Stibitz's "breadboard" circuit would later be given the whimsical name "Model K"-for the kitchen table on which it was assembled. Neither Stibitz nor Zuse knew of each other's relay circuits until after the end of the war, by the way.)14

Years later Stibitz was asked to recount his first steps toward building a relay computer. He said he first learned of binary arithmetic from an algebra textbook he read as a schoolboy in Ohio-a textbook that his mother, who had taught algebra, gave him.15

Of course binary arithmetic follows naturally from the on-or-off nature of a telephone relay, as Zuse recognized, but remember that telephone networks also used a number of ten-position relays that Stibitz certainly knew of. The few other contemporaries of Stibitz (and Zuse) who were modifying telephone equipment to do arithmetic also regarded the relay as a substitute for the ten-position decimal wheels of a mechanical calculator; so they used multi-position relays.16

Only after he had built some of these test circuits for binary arithmetic did Stibitz seriously think of applying them to a complex number machine. Another Bell Labs mathematician, T. C. Fry, mentioned the problem of complex arithmetic to him later that year, and that was how the project got going.17

BUILDING THE COMPLEX NUMBER COMPUTER

Consider once again the formula for multiplying two complex numbers:

(a, b) x (c, d) = (ac-bd, ad + bc)

where the letters a, b, c, and d stand for ordinary decimal numbers of up to eight digits precision. For the moment disregard the position of the decimal point in each number. (Another way of writing the complex number (a, b) is (a+ bi), where i is the square root of -1. If one were to carry out the product of (a + bi) x (c+di) just like an ordinary polynomial, the result would be:
Reckoners, Bell Labs, page 0080 

        a + bi
     x  c + di
       -----------------
        ac + bci
      +            adi + bdi2
       ----------------------
        ac + (bc+ad)i + bdi2
But since i2 = -1, we have ac + (bc+ad )i - bd, or (ac -bd ) + (bc+ad )i, which is the equivalent of the other definition of the complex product.)

Carrying out that multiplication on a machine would require the following steps, in a similar order: 
Operator's actions:
    1.   Key in a, store in machine.
    2.   Key in b, same way.
    3.   Key in c, same way.
    4.	 Key in d, same way.

Machine's actions:
    5.   Multiply a by d, store product temporarily.
    6.	 Multiply a by c, same way.
    7.	 Multiply b by d, same way.
    8.	 Multiply b by c, same way.
    9.	 Add the results of steps (5) and (8), above, 
         giving the imaginary part of the product. 
         Store this result temporarily.
   10.   Subtract the result of step (7) from step (6), giving the real part.
   11.   Display or print the real part, above.
   12.   Display or print the imaginary part, from step (9).
   13.   Stop the machine, and prepare it to accept new input data, if necessary.

There are, then, thirteen basic steps in multiplying two complex numbers automatically. Note that the above order can be varied: by careful attention to detail it is possible to telescope some of those steps together, and minimize the number of temporary storage registers needed.

One important aspect of complex multiplication is that there are no choices involved in the computation: the sequence proceeds the same way each time regardless of the outcome of previous steps. Another aspect is that, of the thirteen steps outlined above, six involve input or output operations-almost half the total. That is a much higher ratio than was found in either the Zuse computers or the Harvard Mark I.

That aspect of complex multiplication meant that if the machine were to handle numbers in the binary scale, a considerable amount of computing would be required to convert numbers to and from the decimal scale for each input or output step. For the Zuse computers that was less of a problem, since they were designed to handle arbitrarily long sequences in which the numbers were "among their [binary] fellows."18

The Complex Number Computer was not programmable. A combination of relay circuits permanently controlled its sequence of operations. Those relays were of the same type as the ones used to handle the numbers, but the machine did not have a separate, clearly defined part that handled the "control" of the computing sequence. (Later Bell Labs computers did.) The concept of programmability arose at Bell Labs only after the Complex Number Computer was built, after its builders saw that its basic computing elements were unduly restricted by its marriage to control circuits tying it to nothing but complex arithmetic. (Besides complex arithmetic, they tried to get the machine to perform polynomial arithmetic, of which complex arithmetic is a special case, cf. above. But the machine was too restricted for that.)


Reckoners, Bell Labs, page 0080

The practical consequence of the machine's permanent program was that it would not make sense to convert numbers into binary for internal handling. So although the first relay circuits Stibitz built were binary, he retained decimal arithmetic for his proposed complex number machine. But he did not want to abandon the simplicity of the binary relay and go over to ten-position relays. So he chose to represent each decimal digit by a tetrad of binary digits. (Four binary digits can express quantities up to 24 = 16.) In this way a group of only four binary relays handled each digit, thereby retaining the simplicity of the binary system at least in the physical construction of the machine. By using the socalled Binary Coded Decimal (BCD) form, Stibitz said, "most of the advantages of the binary system are retained without its disadvantages."19

At one time he thought of training the machine's operators to think in binary, but Stibitz quickly saw that the difficulties of training human beings to work in a different number base would defeat the whole purpose of automating the process in the first place. A few modern computers, especially the very small ones, still must be programmed in binary or a related base, such as 8 or 16.20

Actually, telephone engineers had hit upon binary coding before Stibitz gave it a formal treatment. Switchboards have panels of lights that indicate telephone numbers. The easiest way to construct the panel is to have one wire for each light, or a total of ten wires for each decimal digit, seventy wires for a seven-digit telephone number. But engineers realized that the same information could be carried by only twenty-eight wires, coding each digit on a group of four wires. By the 1930's such an arrangement was standard for the design of telephone switchboards.21


Reckoners, Bell Labs, page 0082

Four wires can code more than ten digits-they can represent up to sixteen. For decimal digits there is a choice of which codes to use and which to ignore. The obvious code would be to have each decimal digit represented by its binary value, that is:


0 coded as 0000
1 coded as 0001
2 coded as 0010
3 coded as 0011
9 coded as 1001

The decimal number 345, for example, would be coded as:
0011 0100 0101

Translating each digit into its BCD equivalent is simple and direct. Each digit key can have a set of four contacts that make the proper coded connection whenever the key is pressed (see Figure 4.1).

The disadvantage of BCD is that it is slightly less efficient than pure binary. Representing a decimal number in pure binary requires a little over three times the number of binary digits, but it takes four times the digits with BCD.

Since 24 = 16, there are many other ways of encoding a decimal digit by a tetrad of binary digits besides the obvious one of using the direct binary equivalent. In fact there are over 29 billion possible ways (the permutation of sixteen items taken ten at a time, which is exactly 29,059,430,400). Whether or not any of those codes offer advantages that the direct binary code does not has been intensively studied in recent years, but in 1938 Stibitz had little theory to guide him.22
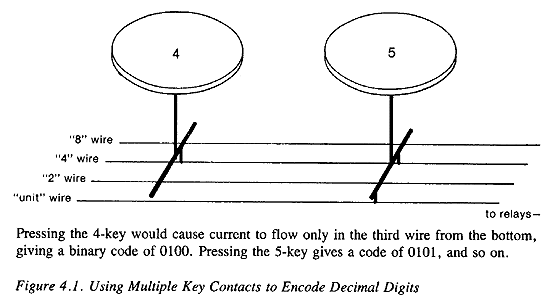
Reckoners, Bell Labs, page 0083

One factor that influenced his choice was the need to have a carry signal; when the sum of the decimal digits was greater than 9, he wanted the code to indicate that somehow. The binary code for 10 is 1010. To have that code initiate a carry would require extra circuits, it seemed.

In a pure binary register, a carry would occur after the number 1111 (decimal 15). That is six greater than the corresponding BCD value of decimal 9 (binary 1001). So Stibitz proposed distributing this difference for his decimal code. In other words, he coded each decimal number by the binary representation of three greater than that number, leaving a gap of three binary numbers at the beginning and at the end of the scheme,viz.: 
      nothing coded as binary 0000 to 0010
      0 coded as 0011 (0 + 3 = 3)
      1 coded as 0100 (1 + 3 = 4)
      2 coded as 0101 (2 + 3 = 5)
      3 coded as 0110 (3 + 3 = 6)
      ...
      ...
      9 coded as 1100 (9 + 3 =12)
      nothing coded as 1101 to 1111

Adding 1 to 9 now looks like: 

      1100
    + 0100
      ----
      0000 plus a carry signal
That is a much easier way to detect a carry than one in which some digits are converted but others are not, depending on the particulars of a specific computation. Since 0000 has no numerical value in excess-three coding, it is easy to recognize when a carry has taken place.

Another advantage to using the excess-three code is that the complement of each digit (the difference between the digit and nine) is obtained simply by exchanging all the ones and zeros: 
     0011 = the code for 0; its complement is 9, coded as 1100
     0100 = the code for 1; its complement is 8, coded as 1011
     0101 = the code for 2; its complement is 7, coded as 1010
      ...
     1100 = the code for 9; its complement is 0, coded as 0011

Reckoners, Bell Labs, page 0084

As we have seen with the Harvard Mark I, most machines do subtraction by adding complements. With the excess-three code those complements are easily obtained, by inverting the state of each relay. So with one stroke, Stibitz preserved a lot of the simplicity of the binary system, while gaining the advantages of handling decimal numbers.23

The remarkable advantages of excess-three arithmetic are not due to any deeper mathematical property of numbers, as far as I know. Modern electronic calculators use BCD, for the same reasons Stibitz used it-calculators have to display their results and receive new numbers frequently. And most of them use the excess-three coding. (Computers, on the other hand, use pure binary, although many of them can be set up to handle binary-coded decimal as well.)

THE COMPLEX NUMBER COMPUTER

Sometime in the fall of 1937 Stibitz drew up plans for a complex number computer using the above coding scheme. Bell Labs approved, and construction began in November, 1938, under the direction of Samuel B. Williams. Stibitz's role was one of developing the logical flow of numbers and operations that the machine was to carry out, and of translating those expressions into designs for relay circuits. Williams in turn applied his knowledge of relay technology to decide how best to construct the circuits that Stibitz had designed. The two men's skills complemented each other. But their roles were not so specialized that each did not help out with the other's work.

Besides deciding on the excess-three, binary-coded-decimal representation, Stibitz also chose to fix the decimal point at the beginning of each number, for example, -.xxxxxxxx. The operator would have to adjust the decimal points of the inputs accordingly. At first he proposed that the machine have a precision of seven decimal digits, but later he increased it to ten digits, of which eight were displayed and the other two were used as "guard digits" and thrown away.24

Most of Stibitz's work at that time consisted of writing out the logical expressions for binary arithmetic, then simplifying them until they were in a form suitable for relay implementation.

He did not know that in Berlin Konrad Zuse was doing almost the exact same thing, only for a pure binary, not a decimal, computer. Stibitz did know that Claude Shannon also had studied the correspondence of statements of symbolic logic with binary relay circuits while a graduate student at MIT. Shannon wrote his graduate thesis (published in 1938) on that subject, and then went to Bell Labs, where he and Stibitz learned of each other's work. But Shannon was not actively involved in the design of the Complex Number Computer. Clearly the idea of using relays to implement binary logic was common in the late 1930's. (Also in the 1930's there was a similar discovery in Japan, but that, too, was unknown in both Germany and America.)25


Reckoners, Bell Labs, page 0085

Sam Williams implemented those designs using the latest relay technology available to him. He adapted ordinary ten-digit keyboards for the numerical input, another bank of keys for the control commands, and an ordinary teletype machine for the printed output (Figure 4.2).

Probably his most important contribution was to use the newly-developed crossbar switch to store the four numbers that comprised the input. Crossbars were developed to replace the Strowger rotary switches then in common use; instead of the six or eight contacts that a binary relay could handle, a crossbar had a matrix of switching elements that could switch up to 2,000 individual contacts.26

Construction of the Complex Number Computer began in April, 1939, at the old Bell Laboratories Building at 463 West Street in Manhattan. (Bell Labs moved to New Jersey after World War Two. The old buildings in Lower Manhattan have since become artists' lofts, and the dreary industrial neighborhood now goes by the fashionable name of Westbeth.) The machine was completed in October of that year. It began doing routine calculations for the Labs in January, 1940, and remained in service until 1949. As Bell Labs built other relay computers during the war, its name changed from Complex Number Computer (or "Complex Computer") to "Model 1."27 Table 4.1 lists the full specifications of the machine.


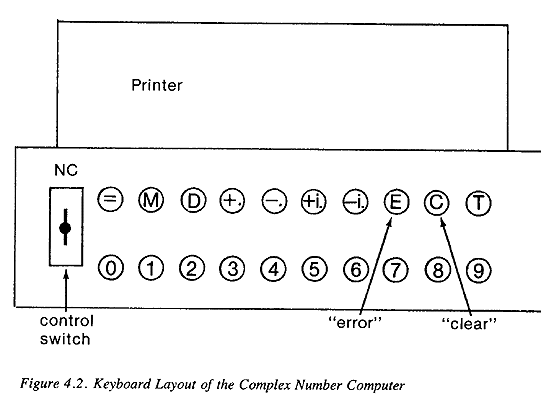
Reckoners, Bell Labs, page 0086

Table 4.1 THE BELL LABS MODEL I

Builders: George R. Stibitz, Samuel B. Williams.
Place: Bell Laboratories, 463 West Street, New York.
Dates: Authorized 1938.
Construction begun April, 1939.
Completed October, 1939.
Began operation January 8, 1940.
Demonstrated to the public September 11, 1940, Dartmouth College.
Dismantled 1949.
Cost: Approx. $20,000.
Technology: 400-450 relays, 10 crossbar switches. 6-8 panels (approx. 8' x 5' x 1').
Arithmetic: 8-digit precision (10 internally), range ±0.99999999.
Binary-coded-decimal, excess-three code.
Fixed decimal point at beginning of number.
Programming: Fixed program to perform the four operations of complex arithmetic.
Sequential operation; i.e., each relay or set of relays would commence its operation immediately after the relays before it in the sequence were finished. There was no synchronizing clock.
Speed: Approximately one minute per multiplication.
Input/Output: Ordinary teletype with a modified keyboard. Teletype connected to processor by a multiple-wire buss; therefore remote operation was possible. Up to three teletypes were connected to the arithmetic unit; an interlock permitted only one to be active at a time.

EVALUATION OF THE MACHINE-ANATOMY

The Complex Computer used relays as its basic building block-that was its "anatomy." Its appearance was deceptively simple: a metal rack for the relays, teletype keyboards for the input and output.

In a relay computer the structure is in the way the wiring is routed from one relay in the cabinet to another. One cannot discern the functions of those relays simply by looking at their position on the rack. The Harvard Mark I's layout by contrast was constrained by the need to have its elements arranged along a common driveshaft. Its structure was more revealing of the way it functioned, but at the same time it was not easy to modify that structure later on.


Reckoners, Bell Labs, page 0087

The Complex Computer was originally designed to compute only complex products and quotients; sums and differences were thought easy enough to be done manually. But soon after the machine was completed Williams realized that if the machine's registers were not cleared immediately after a multiplication it could accumulate sums as well. He added that modification with little difficulty to add or subtract complex numbers the operator disabled the clearing function, keyed in the number to be added or subtracted, then "multiplied" it by either + 1 or-1 (in complex form (1, 0) or (-1, 0)) to add or subtract.

Stibitz and Williams made another modification to the machine shortly after it was completed. They found that by disabling another clearing relay, the machine would multiply a number by a list of other numbers without having to key in the first number again and again. Stibitz first improvised this constant function by jamming a toothpick (!) in the relay that did the clearing; later the function was permanently wired in, with an appropriate button on the keyboard to activate it.28 (It is surprising how frequently computer users today modify their million-dollar machines in the same kind of ad hoc ways, not always with the blessings of the computer manufacturer-recall Thomas Watson's desire to have the Harvard Mark I enclosed in steel and glass. But mechanical brains are, after all, machines, and there is no reason why their brass cannot be bent to serve man's will. Just the same, it takes some courage to make a so-called kluge modification to a computer, as Stibitz did.)

Using crossbar switches as number registers no doubt simplified the computer's construction, but it also limited its flexibility. Crossbar switches were much more complex than simple relays; they were also slower. All of the later Bell Labs relay computers used only simple relays for their construction.29

The binary-coded-decimal scheme is a hybrid, and it shares some of the properties of both binary and decimal arithmetic. Fundamentally, a decimal machine is a decimal machine, regardless of the code used for the individual decimal digits, since that is the way arithmetic is done internally. For example, the registers of the Complex Number Computer initiated a carry after the number 9, not after 1. The machine performed multiplication by repeated addition, but in its preliminary design phase there was some discussion over whether or not a table look-up might be better (cf. the Mark I). We have already seen with the Zuse computers that with a pure binary representation there is no difference between the two methods.

Some aspects of the machine's number handling were more suggestive of the binary system, however. When two numbers were added to each other, the register proceeded immediately to their sum, as a binary register does (and as human beings do). It did not pass through all the intermediate numbers before arriving at the sum. The Complex Number Computer thus computed sums in registers; it did not accumulate them like the Harvard Mark 1. That was in part a consequence of the binary nature of the relays used in the machine; like the Zuse computers it handled numbers by applying the rules of symbolic logic. That is one step further removed from our ordinary intuitive concept of number.30

Figure 4.3 shows the structure of the Model I in block form. Of course the machine had no separate programming unit, so the circuits that directed the sequences of operations do not show up in the diagram, as they were scattered throughout the other units.
Reckoners, Bell Labs, page 0088

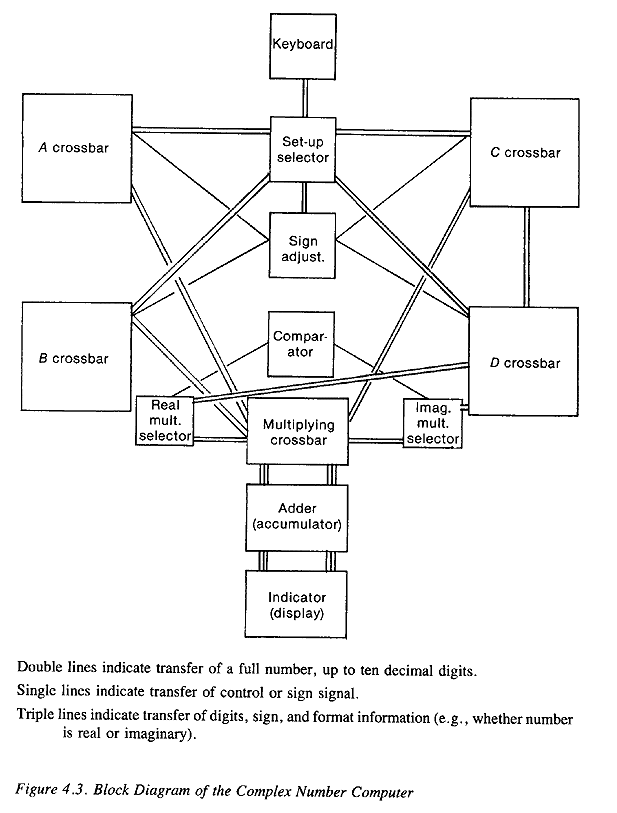Figure 4.3. Block Diagram of the Complex Number Computer
Reckoners, Bell Labs, page 0089

EVALUATION OF THE MACHINE-PHYSIOLOGY

The best way to see how the Complex Computer worked is to follow a typical problem and trace the steps it takes to solve it.

Assume the operator wants to divide the complex number (0.33 + 0.99i) by (-0.370 + 0.91i). This example is one Stibitz himself gave in a public demonstration, using the letter i to indicate the "imaginary" part of the number. Note also that he had already put the numbers in "normalized" form, with the decimal point at the beginning, since that was where the machine assumed it would be. In most problems the operator had to mentally scale the numbers until they were in that form-that was a limitation of the machine's power, and one which Stibitz and Williams recognized as being a serious one. But they chose not to modify the machine to let the decimal point float, as that would have required too much redesign. But even as the Complex Number Computer was performing its first calculations, they were working on a proposed "Model Two" that would have floating point.31

The operator was seated at a modified teletype terminal (see Figure 4.2, above). In the Bell Labs Building there were three of those terminals, each connected to the computer. The computing unit itself was kept in an unattended room in the building; few persons who used the machine actually saw it. The operator connected her terminal to the computer by flipping a switch on the left of the keyboard (I use the feminine pronoun because men seldom operated the computer). If another terminal was already in use, hers would be "locked out" -access denied-as a telephone caller gets a busy signal when the person being called is already on the line to someone else. As a rule, they used the machine only for brief sessions, perhaps a few multiplications or so, so the operator would usually wait a few minutes and try again. This early example of remote, multiple access illustrates the kind of flexibility and easy access that relay computers often had.

Having gained access to the machine, the operator would key in the problem as follows:

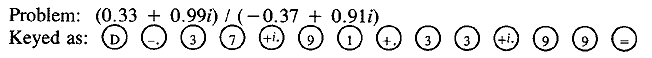
Note that the order is not the same as that in which the problem is usually stated. Pressing the key D told the machine that a division was to be performed, and would close certain relays that prepared the machine for that operation. The Complex Number Computer used "Prefix" notation-the operation was keyed in before the operands, not in between them, as a division is usually written, nor after them, as the Zuse computers did.
Reckoners, Bell Labs, page 0090


Reckoners, Bell Labs, page 0091

In a division the operator keyed in the denominator before the numerator, as the example shows-again the opposite of the way it is usually written. That was because in the formula for complex division, the quantity (c2 + d2) is required for both parts of the answer. Keying in the denominator first got those numbers into the machine first, so that it could begin computing the "norm" (CZ + d2 while the operator was keying in the numerator. Like the Mark I, the Complex Computer had quite a bit of parallel computing capability, and that helped speed up the operation of division. By keying the (@ key, the operator alerted the machine that she was finished keying in the real part, that the imaginary part was to follow, and that the imaginary part was positive. The decimal point after the i appeared on all the sign keys, since all numbers had to begin with a decimal point.

After keying in the imaginary part of the denominator, the operator keyed +O. , which told the machine that the real part of the numerator was to follow. As soon as she pressed that key the machine would begin computing the norm, since it "knew" that all the digits of the denominator were in the machine. (It automatically added trailing zeros into the registers; for instance, -.37 was stored as -.37000000, but the operator did not have to key the trailing zeros in.)

Finally the operator pressed the (E) key, upon which the machine would immedately begin printing the quotient in the following format: 
        - .37000000 + i.91000000 \ + .33000000 + i.99000000 
        =  + 0.80704663 -i.0.69077720
Note the special reversed division sign. I say that the machine began rinting its answer immediately because as soon as the first number, -.37 was entered, printing began. The input numbers were printed while the answer was being computed. The average speed was estimated as "three times as fast as a human being equipped with a desk calculator," or about half a minute for a division.32

Some other samples of the machine's abilities were published in Science News Letter in September, 1940, including the following: 
         + .45632450 + i.45367899 \ + .31612848 + i.20028853
         = +0.56785431 -i.0.12564532
The machine truncated, not rounded, its results to eight digits; otherwise the last digit of the complex part of the answer would be a 3, not a 2.

The article also showed how the machine would multiply 2 x 2: 
        + .20000000 + i.00000000 x + .20000000 + i.00000000
        = 0.04000000 +i.00000000

Reckoners, Bell Labs, page 0092

The operator had to adjust the decimal points accordingly.33

THE DARTMOUTH DEMONSTRATION

The Complex Computer was not really a computer by the definition I have been using throughout this book; it was not programmable. Nonetheless it rightly belongs among the early computing devices because of other things that made up for that deficiency. First of all, it marked the beginning of Bell Labs in the computing field; later on they would build relay devices that did have flexible programming facilities, including conditional branching and subroutines, as we shall see. Second, the "Model I" just described introduced the idea of automatic digital computing to the mathematics community at an early date, well before the Z3 or the Harvard Mark I were operational. That was in the summer of 1940, at a meeting of the American Mathematical Society at Dartmouth College in Hanover, New Hampshire. This public demonstration was a pivotal moment in the history of computing- it not only was a demonstration of a working digital calculating machine; it was also the first example of remote access to a computer, something that would not be repeated for another ten years. It marks a beginning of "telecommunications"-the use of telephone lines to carry not voice messages, but coded computer data.

The computer was finished by January, 1940. After it had demonstrated its worth for a while, T. C. Fry at the Labs suggested that Stibitz present a paper on it at the summer meeting of the American Mathematical Society. Fry further suggested that Stibitz actually demonstrate the machine at the meeting by having someone dictate problems over the phone to New York, then receiving the answers as the machine computed them.34

Gradually through the summer of 1940 that idea progressed to the notion of having one of the teletype machines actually set up in Hanover, so that the participants could key in the problems themselves. The summer meeting was not to be held until September, so there was time to make the necessary modifications.

Stibitz was not sure he would be able to demonstrate the machine without some human intervention in New York, but that was his goal. He and Fry worked up to the eleventh hour completing the necessary circuits. AT&T set up a twentyeight-wire teletype link between Hanover and New York, and coders and decoders were built at each end. Williams remained in New York during the meeting in case anything went wrong, but everything worked fine without his help.35

The Society met in McNutt Hall on the Dartmouth campus from the 10th to the 12th of September, 1940. New Hampshire is usually at its prettiest in September, but in 1940 the events in Europe dampened everyone's spirits. The meeting was attended by most of the prominent American mathematicians of the day-John von Neumann, G. D. Birkhoff, Norbert Wiener-as well as by John Mauchly and many others who would later be involved in computing projects. (Many participants were, strictly speaking, foreign mathematicians who had taken refuge in America-for example, Richard Courant, Paul Erdos, and John von Neumann. By 1940 many of them had obtained American citizenship. As far as I can tell, there were no German mathematicians who returned to Germany before America's entry into the war.)
Reckoners, Bell Labs, page 0093

On September 11 Stibitz delivered a paper which briefly described how he came to build the Complex Computer, and why there was a need for it at Bell Laboratories. After reading the paper, he and Fry showed how problems were entered on the keyboard by running a few sample ones. The machine took about a minute for each, and it ran without error. Following that demonstration, the audience was invited to submit their own problems via the keyboard. It was available to all from 11:00 A.M. to 2:00 P.M. that day.36

There is no doubt that this demonstration made an impression on many who witnessed it. Norbert Wiener, for example, played with it for a while, testing its logic by trying to divide by zero and the like. But he was unable to get the machine to give an incorrect answer, and later, in his autobiography, he recounted that experience at length. It must have been one of his first exposures to the "thinking" properties of machines. Later on he submitted his own proposal to Vannevar Bush for a digital computer, but he was turned down. He spent the war years at MIT doing work that was related more to analog than to digital computing.37 The Hanover demonstration was also reported in the popular press, but it is clear that Bell wanted most of all to introduce its computer to the mathematics community.

Remote access to computers is common today, but after the Dartmouth demonstration it was not done again until 1950, with the SEAC in Washington, D.C. The demonstration also foreshadowed a time when high-speed data (as opposed to voice) communications would be an integral part of the Bell System's trafficnot to mention that of Bell's competitors. In fact, it is in the area of telecommunications, not voice traffic, where Bell is presently most seriously threatened by competition. But that is another story.

AFTER THE MODEL I: LATER DEVELOPMENTS

Bell Labs took only a moderate interest in Stibitz's work. They were interested in machines that could solve specific problems, but they did not see building general-purpose computers as a worthwhile goal in itself. As the Complex Number Computer was nearing completion, Stibitz was designing machines with more advanced features such as floating point and suppression of leading and trailing zeros. Above all he recognized that it would not be difficult to program future relay computers by paper tape and so not restrict them to only one specific problem.

His proposal to build a successor to the Model I, a relay computer that would be programmable by paper tape, was at first rejected. Then the United States entered World War Two in December, 1941. Bell Labs found itself facing a new set of priorities. Domestic phone service was not among them, but projects involving computing were.38

Bell Labs began working on devices that aimed antiaircraft fire. The result was
Reckoners, Bell Labs, page 0094

the famous M-9 Gun Director, an ingenious combination of electronic circuits (rugged enough for the battlefield), electric motors, electrical sensors, and mechanical linkages that helped a gunner track a moving target in the sky and hit it (like shooting ducks only a lot more complicated). The M-9 was ingenious, and it worked well. It was especially effective in blunting the effect of the German V-1 "buzzbomb" over England and the Low Countries in the later years of the war-the buzzbomb had no pilot and so could not take evasive action against Allied antiaircraft fire.39

In this and other computing projects the government was willing to underwrite development costs for new and untried technology. Stibitz moved to the National Defense Research Committee (NDRC), under the supervision of Warren Weaver, but he still kept close ties with Bell. For the duration of the war his main job concerned the design and use of programmable digital calculating machines.

Bell Labs paralleled IBM's building of the Mark I in its first steps into the large-scale computer world: both considered the computer as being far outside their normal sphere of business, but both entered that field and built computers that contributed to the war effort. But the projects themselves were funded mostly by the United States government.

The machines designed by Stibitz and built by Bell Labs after 1940 exhibited two significant qualities: programmability and reliability. All in all, Bell Labs built six more relay computers after the Complex Number Computer, and a chronicle of their development shows a steady progression toward more flexible programming and better techniques for detecting and correcting errors.

For the testing of the M-9 Gun Director it was necessary to run it through a simulated firing, then see whether it in fact kept the gun aimed as it was supposed to. That led to a lot of calculations, especially ones involving the reading of tables of function values and the interpolation of intermediate values from those tables. Stibitz proposed building a relay machine to interpolate function values, and in 1943 the so-called Relay Interpolator was the result. (Later it would be called the Bell Labs Model II.)

The relay interpolator performed only addition and subtraction but by repeated addition it could multiply a number by a small integer as well. However, it could be programmed by paper tape, unlike the Model I, so it had quite a general capability. After the war it was kept in service and used for a few other problems besides interpolation.40

Stibitz then desgned two more special-purpose relay machines for the NDRC: the Ballistic Computer and the Error Detector Mark 22. Both machines were concerned with detecting and minimizing the error in aiming antiaircraft fire at a moving target and having the shell explode at precisely the right moment. (They were later renamed the Bell Labs Models III and IV respectively.) Like the Model Il, they used a standard five-channel paper tape for the input of data and instructions; unlike the Model II, they were often used for many other problems besides the specific ones they were built to solve. Their memory and arithmetic units had modest capabilities: only six decimal digits of precision, a memory of
Reckoners, Bell Labs, page 0095

ten numbers for each machine. They performed multiplication by referring to an internal table of decimal products, unlike the slower method of repeated addition used on all other Bell Labs machines. The result was that they were well-balanced machines whose power, speed, reliability, and ease of programming allowed them to tackle tough problems. Those who used the Models III and IV always spoke well of them; the machines seemed to have just the right balance of features for their relay technology-in contrast to the Models I and 11, which were too limited in power, or to the Model V, which was designed for work that was really more appropriate for electronic computers.41

Stibitz built one more machine for the NDRC: the Model V, a large-scale general-purpose relay computer in the same league as the Zuse Z4 or the Harvard Mark 1. It was not completed until after the war, in 1946, after which Stibitz left that government agency. Two identical copies of the Model V were built, one installed at the Aberdeen Proving Ground in Maryland, the other at the National Advisory Committee on Aeronautics' laboratory at Langley Field, Virginia.

Bell Labs built one more machine, the Model VI, which was a simpler version of the Model V. The Model VI was the only relay machine besides the Complex Number Computer that they kept for their own use; the others were for the military. Table 4.2 summarizes the specifications of the Models 11 through V.

Table 4.2. BELL LABS MODELS 11 THROUGH V
. Model 11 Model III Model IV Model V
(two copies)
Date completed 7-19436-1944 3-1945 12-1946, 8-1947
Date dismantled 1961 1958 1961 1958
Place installed Wash., D.C.Ft. Bliss, TexasWash., D.C.Langley, Va.
Aberdeen, Md.
Also known as Relay
Interpolator 		Ballistic
Computer 		Error Detector
Mark 22
No. relays 440 1,400 1,425 9,000+
Word length 2 to 5
fixed decimal 		1 to 6
fixed pt. 		1 to 6
fixed pt. 		1 to 7
floating pt.
Memory cap. 7 numbers 10 10 30 total
Mult. speed 4 sec. 1 sec. 1 sec. 0.8 sec.
Mult. method repeated add. table look-up table look-up rep. add.
Cost . $65,000 $65,000 $500,000
Size 2 panels 5 panels 5 panels 27 panels
10 tons

Reckoners, Bell Labs, page 0096

The Model V was a powerful machine. But by the time it was finished in 1946 attention was turning toward the much faster vacuum tube technology. So it represents in many ways the limit to what can be done with relay technology. Because of its flexible programming power and its built-in reliability circuits it was able to keep up with the much faster electronic computers for many applications, but those kinds of features could also be added to future electronic machines, whereas there was no way to increase the intrinsic speed of relay computers much beyond what the Model V's relays had.42

The most interesting aspect of the Model V's design was that it had two separate arithmetic units, each capable of operating as an independent computer with its own memory registers and input-output devices. Small-scale problems could be run in pairs on the machine, saving time, while bigger problems could take over both processors. (Some confusion has arisen about the Model V because of this arrangement: each processor was called a "computer" in the literature describing the Model V. Today they would be called "processors.") Associated with each processor (using the modern term) were fifteen memory registers, for a total of thirty for the whole machine. A master control unit directed instructions to one or both processors according to their availability. This control unit was separate from the control units in the processor that directed the sequence of arithmetic, memory, and input/output operations; it controlled the control, so to speak. (Stibitz called it a "superbranching" capability.) Thus in a very real sense the Model V had what is now called an "operating system"-a control unit that supervises and manages the flow of work through a computer. (Operating systemsmuch more sophisticated, of course- became commonplace in the third generation of large computers, after 1965.)

The flexibility provided by superbranching allowed the Model V to out-perform the much faster electronic computers for certain problems. It obviously added to the machine's cost and complexity. Its successor, the Model VI, designed for Bell Labs' internal use, had only one processor.43

RELIABILITY

Besides programming power, the later Bell computers stressed extraordinary reliability. The Model I was checked by running selected problems whose answers were known beforehand at the beginning and end of each day. (That was also done on the Harvard Mark I every few hours.) If the machine gave correct answers to those "diagnostic" problems (which were specially formulated to put all the pieces of the machine through their paces), then its users could be reasonably sure that the answers it gave between those diagnostic sessions also were correct.44


Reckoners, Bell Labs, page 0097

But that approach had its obvious drawbacks. Long problems had to be interrupted every so often, intermediate data saved, then a diagnostic run. And if the diagnostic program revealed a mechanical failure, all the work going back to the last diagnostic session had to be discarded, since there was no way of knowing exactly when the failure occurred.

For very fast machines which execute long programs that is a serious drawback. It is even more serious for machines like the Bell computers that used telephone relays. In contrast to mechanical devices or to electronic tubes, relays have a tendency to fail intermittently. Should a piece of dust lodge itself between two relay contacts, that circuit will fail, though the rest of the relay will be fine. After a few cycles, the dust particle may shake itself loose, after which everything will return to normal. Thus an entire computation may be way off without any machine failure showing up during a diagnostic session. By contrast, when a vacuum tube or a mechanical cam fails, it (usually) stays that way, so a failure is more easily isolated and corrected.

Other than that kind of intermittent failure, relays are reliable devices. They are well suited for ordinary telephone circuits, where the loss of a few seconds of a conversation or an occasional bad connection is tolerable. But for a computer that is intolerable. Bell's engineers recognized that a computer system should shut down completely when any of its circuits failed, as that usually meant the machine was delivering wrong answers. (By contrast, telephone users do not like their phone service shut down at all if it can be avoided-even if that means accepting poorer service.)45

So a philosophy of reliability emerged at Bell Labs that reflected the difference between computing and telephony. Bell's engineers designed computer circuits that checked themselves at every step of a computation, like policemen looking over everyone's shoulder. The circuits were designed not only to add, subtract, store numbers, and so on; they were also designed to check that they had done those things correctly, and to stop the machine otherwise.

Bell's engineers were also guided by their experience in designing telephone circuits that had to operate long hours unattended in often hostile environments. Those circuits were designed to be repaired by semi-skilled technicians; telephone service would be terribly costly if an engineer had to be called in every time a phone line went down or a customer's phone went dead.

The Bell Labs Models II through VI used a system whereby not four but seven binary relays coded each decimal digit. They were divided into two groups of two and five relays; the decimal code was as follows: 
	Decimal digit		Relays
	0		01		00001
	1		01		00010
	2		01		00100
	3		01		01000
	4		01		10000
	5		10		00001
	6		10		00010
	7		10		00100
	8		10		01000
	9		10		10000

Reckoners, Bell Labs, page 0098

A special circuit checked to see that two and only two relays were energized for each decimal digit. Another circuit checked that for each group one and only one relay was on- that prevented two separate errors from canceling each other out, although certain unusual combinations of malfunctions could go undetected.

Bell Labs called this system a "bi-quinary" notation, since the relays had a weight of either one or five. Actually, it is not a combination of those number bases; rather, it is a seven-bit, mixed decimal code. All the Bell Labs relay computers worked in decimal arithmetic.46

Note the similarity of the bi-quinary code to the weights of the beads on a Chinese abacus: beads above the divider bar have a weight of five, those below a weight of one. (Stibitz has said recently that he first realized that the bi-quinary code was similar to the Chinese abacus only after he had designed the relay codes, when someone else pointed it out to him.)47

The bi-quinary system was an empirical way of adding redundancy to a circuit to give it more reliability. It worked well for representing decimal numbers but it could not easily be generalized to other types of machines or to other number bases, including binary. Using Stibitz's work as a starting point, Richard Hamming of Bell Labs generalized the concept of error checking and developed a theory that guided computer designers thereafter. That was the so-called paritychecking scheme, which is valid for any coded information in any number base. Using parity checking, an extra binary element (relay or whatever) is added to each code, and that element is turned on or off to make the total number of binary elements "on" an even or odd number, as specified in advance. A separate circuit checks whether that sum is even or odd, and stops the machine if the sum is wrong.

Hamming went on to show that if more redundancy was added to a number code, it could not only detect errors but also correct them as well. He worked out the trade-offs of each redundant bit added, and his work has formed the basis for nearly all computer circuit design ever since. It is so integral to modern computers that "only the old-timers are still conscious that somebody once invented it."48 (One consequence of parity checking is that commercial computers today cannot, strictly speaking, err. They may malfunction, but they cannot deliver the erroneous result 2 + 2 = 5 unless programmed to do so. What is so often called "computer error" in the popular press is more correctly the result of human errors of programming or of giving the machine the wrong input data. That misperception is unfortunately too current among the lay public today. Only a few specialpurpose or experimental computers, like the ILLIAC IV, do not use parity checking.)

In a discussion of the Model V, Hamming said that it had on the average two to five relay malfunctions per day, or the equivalent of one failure for every two to three million relay cycles. If a failure occurred during the day, when an operator was present, the machine would stop; otherwise it would automatically transfer control to its other processor and take up whatever problem was residing there. Thus there was almost no down-time for the Model V.49
Reckoners, Bell Labs, page 0099

POSTWAR ACTIVITIES AT BELL LABS

Bell Labs built the Model VI for its own use after the war. (When it was placed in service at their new headquarters in Murray Hill, New Jersey, in 1949, they dismantled the Model I.) The Model VI used the bi-quinary number code, had full conditional branching and subroutine capability, but lacked the dual processors and superbranching power of the Model V. The Model VI marked the end of Bell's role as a builder of relay computers. By 1950 the trend was clearly toward vacuum tubes for computing elements, and that was a technology less familiar to Bell's engineers. The two Model V's and the Model VI were unmatched for their reliability and flexibility in programming, but their speed was on a plateau at least an order of magnitude below even the slowest electronic computers, and that more than offset their advantages.50

A tremendous backlog of domestic telephone orders had built up during the war. It was the time of suburban sprawl, as returning G.I.'s and their families moved into Levittowns and other housing tracts across the country. Those suburbs needed telephone service, and until the early fifties Bell's resources were strained to the utmost in providing it. Stibitz left Bell Labs during the war and did not return. It was not at all clear where digital computers fit into Vail's dictum of "one system, one policy, and universal service." Bell was (and is) a regulated monopoly whose every action was always noticed by the government and by its competitors. Whatever the reason, Bell Labs chose not to go into the business of making and selling electronic digital computers.51

But the company was active in other ways, one of which was revolutionary. That was the invention of the transistor in 1948, by William Shockley, John Bardeen, and Walter Brattain. Bell Labs had been working on a solid state amplifier to replace their vacuum tube circuits for a long time. The transistor was the result of that search.

Bell intended to use the transistor as an amplifying device for long-distance lines. But like the tube, it could also be used as a digital switch and thus replace their relays as well. But there was little need for that in 1948.

So while the transistor was successfully employed in telephone amplifiers, it was in the commercial computing industry and not in the Bell System where it first found application as a digital switching device. The first transistors were no more reliable than the tubes or relays they were supposed to replace, but by the late 1950's computer manufacturers adopted them wholeheartedly. They were smaller and less prone to fail than tubes; above all they gave off little heat, and that was a big advantage over tubes. Bell Labs had a lot of capital invested in their relay technology; they embarked on a plan of slow and gradual replacement by transistors as the relay circuits wore out. Relay switching is still common today in the telephone system.

Bell Labs saw the potential advantages of transistors for computers-they built one of the first transistorized computers in the world, the TRADIC, in 1955. But they did not go into the commercial computer business.52
Reckoners, Bell Labs, page 0100

In 1949 AT&T began fighting an antitrust suit brought against them by the Justice Department, which sought to allow other equipment manufacturers besides Bell's own Western Electric to supply equipment to the Bell System. AT&T fought the suit vigorously, contending that as a regulated monopoly it was exempt from antitrust laws concerning such tie-in agreements. The suit was settled by a Consent Decree between Bell and the Justice Department in January, 1956, by which the Bell System's monopoly structure, including its ownership of Western Electric, remained intact. In return, Bell agreed to enter into no "business other than the furnishing of common carrier communications services."53

Going into the computer business seemed to be just the sort of non-communications activity that they agreed to stay out of-although the boundaries between computing and communications are much less clear today. The Bell System continued to supply telephone service; other, nonregulated companies built and sold computers commercially. As the technologies of both evolved, the two activities grew closer to each other, but Bell found itself restrained from moving aggressively into new areas of telecommunications that ironically it had pioneered. (In 1981 that Consent Decree was overturned; in exchange the Bell System will be broken up. Among other consequences, Bell Labs in now free to design and market commercial computers. Whether they will or not is hardly clear; but they certainly have the technical ability to do so. In fact, they may be the only company today with the financial strength to compete with IBM head-to-head.)

Another provision of the 1956 Consent Decree was that Bell Labs agreed to make its patents on the transistor freely available to companies who wanted to manufacture and sell them. A number of companies responded, and within a short time transistors became widely available, more reliable, and cheaper.53 The next phase of the computer revolution began-the phase in which computers have become dramatically cheaper, smaller, and more integrated into all parts of modern American life. That phase is still going on apace.

Today's telephone system uses a variety of special-purpose digital computers for things like switching, while for other jobs like billing it uses ordinary commercial computers. AT&T is one of IBM's best customers; it also buys a lot of computers from the other manufacturers as well. Bell Labs designs and builds computer chips for their own use, and for those chips they have developed powerful and sophisticated programming tools (for example, the "C" programming language and the UNIX operating system). Whatever else may be said about Bell Labs' position in the modern computing world, they were involved in computing from the start of the age, they still are involved, and there is little question they will continue to be involved.

In conclusion, the story of Bell Laboratories' role in the invention of the computer is one of significant contributions in many areas. These are:
  1. The coding of information as a subject of theoretical interest in itself. From Stibitz and Claude Shannon came a notion of information as a quantity that can be treated like any other abstract quantity, as it is processed, transmitted, and coded in machinery.
    Reckoners, Bell Labs, page 0101

  2. The binary-coded-decimal system of coding numbers, still widely used where information is input or output frequently by a machine.
  3. The design philosophy of incorporating redundancy in a computer code to ensure error-free operation, thus relieving the user of the burden of testing the integrity of the system's hardware.
At the same time it is clear that Bell Labs stands outside of the direct ancestral line that leads to the modern computer. In part that is because they were a regulated monopoly, in part because the relay technology they knew best was seen as unsuitable for computers after 1950. But they were, and are, pioneers just the same.



NOTES

  1. Gerald Brock, The Telecommunications Industry: The Dynamics of Market Structure (Cambridge, Mass.: Harvard, 1981), chapter 4; John Brooks, Telephone: The First Hundred Years (New York: Harper & Row, 1976), pp. 138-139.
  2. Lillian Hoddeson, "The Emergence of Basic Research in the Bell Telephone System," Technology and Culture, 22 (1981), 512-544.
  3. A few phone systems around the country still have no dial of any type: the user must turn a crank which signals an operator at a central switchboard. Those few that survive may ironicallybe preserved as living museum pieces; see "Save Crank Phones? Mainers Split at Hearing," Boston Globe, February 12, 1982, pp. 15, 17.
  4. Melvin Kranzberg and Carroll Pursell, eds., Technology in Western Civilization, vol. 1 (New York: Oxford, 1967), pp. 644-645; Brooks, Telephone, pp. 100-101.
  5. E. G. Andrews, "Telephone Switching and the Early Bell Laboratories Computers," Bell System Technical Journal, 42 (1963), 341-353.
  6. Hoddeson, "Basic Research," p. 530; Brock, Telecommunications, p. 102.
  7. E. G. Andrews, "Telephone Switching," p. 343.
  8. Jagit Singh, Great Ideas of Modern Mathematics (New York: Dover, 1959), pp. 12-13.
  9. Norbert Wiener, 1 Am a Mathematician (Cambridge, Mass.: MIT, 1956), p. 75; David E. Smith, History of Mathematics, vol. 2 (New York: Dover, 1958), pp. 261-268.
  10. Wiener, Mathematician, p. 247; Andrews, "Telephone Switching," p. 343; George Stibitz, memo of August 19, 1938, Box 1, Stibitz Papers, Baker Library, Hanover, N. H.
  11. George Stibitz, memo of August 26, 1938, Stibitz Papers, Box 1.
  12. "An Inventory of the Papers of George Robert Stibitz, Concerning the Invention and Development of the Digital Computer" (Hanover, N. H.: Dartmouth College, 1973; Henry Tropp, "The Effervescent Years: A Retrospective," IEEE Spectrum, 11 (February, 1974), 70-81.
  13. Published in part as "Potentials in Curved Surfaces," Philosophical Magazine, 7th ser., 25 (1938), 783-785.
  14. Tropp, "Effervescent Years," p. 71; Konrad Zuse, Der Computer, Mein Lebenswerk (Munich: 1970), pp. 52-53.
  15. George Stibitz, letter to the author, December 12, 1978.
  16. See, for example, A. Weygandt, "Die Elektromechanische Detenninantenmaschine," Zeitschrift fur Instrumentenkunde, 53 (1933), 114-121.
    Reckoners, Bell Labs, page 0102

  17. G. R. Stibitz and Evelyn Loveday, "The Relay Computers at Bell Labs," Datamation, 13 (April, 1967), 35-44; 14 (May 1967), 45-49.
  18. Konrad Zuse, "Method for Automatic Execution of Calculations with the Aid of Computers," German Patent Application Z-23139 IX/42m, 1939, translated and reprinted in Brian Randell, ed., The Origins of Digital Computers: Selected Papers, 2nd ed. (New York: Springer, 1975), pp. 159-166.
  19. Stibitz, memo of March 28, 1938, Stibitz Papers, Box 1; E. G. Andrews, "Telephone Switching," pp. 342-344.
  20. Stibitz, memo of March 28, 1938, Stibitz Papers, Box 1.
  21. Andrews, "Telephone Switching," pp. 342-344.
  22. Anton Glaser, History of Binary and Other Non-decimal Numeration (Southhampton, Pa.: privately printed, 1971), pp. 135-140.
  23. Stibitz and Loveday, "Relay Computers," p. 35; Glaser, History of Binary, pp. 129- 153; Evelyn Loveday, "George Stibitz and the Bell Labs Relay Computers," Datamation, 24 (September, 1977), 80-85.
  24. Andrews, "Telephone Switching."
  25. Claude Shannon, "A Symbolic Analysis of Switching Circuits," Transactions AIEE, 57 (1938), 713; Hidetosi Takahasi, "Some Important Computers of Japanese Design," Proceedings, First USA-Japan Computer Conference, October 3-5, 1972, Tokyo, pp. 692-697.
  26. Andrews, "Telephone Switching," p. 344; Malcolm Stevenson, "Bell Labs: A Pioneer in Computing Technology," Bell Labs Record, 51 (1973), 344-351.
  27. Stibitz and Loveday, "Relay Computers," pp. 45-48.
  28. Ibid., p. 41; Stibitz, memo of August 19, 1940, Box 1, Stibitz Papers.
  29. Stevenson, "Bell Labs," pp. 345-346.
  30. Glaser, History of Binary, p. 132.
  31. Stibitz, memo of November 1, 1939, Box 1, Stibitz Papers.
  32. Stevenson, "Bell Labs," p. 346.
  33. "Electric Calculating Machine Devised for Complex Problems," Science News Letter, September 14, 1940, p. 163.
  34. Stibitz and Loveday, "Relay Computers," pp. 39, 43.
  35. There are at least five separate drafts of the Hanover paper in Box 1 of the Stibitz Papers, each with a slightly different description of what was to be demonstrated. One draft has been published in Brian Randell, Origins of Digital Computers, pp. 241-246.
  36. Wiener, Mathematician, pp. 229; T. R. Hollcroft, "The Summer Meeting in Hanover," Bulletin, American Mathematical Society, 46 (1940), 861; Andrews, "Telephone Switching," p. 353.
  37. Wiener, Mathematician, pp. 229-240. Wiener gives the date of the meeting as August, 1940, which is incorrect.
  38. Stibitz, memo of August 19, 1940, Box 1, Stibitz Papers; Stibitz and Loveday, "Relay Computers," p. 44; Andrews, "Telephone Switching," pp. 347-348.
  39. Charles and Ray Eames, A Computer Perspective (Cambridge, Mass.: Harvard, 1973), p. 128.
  40. George Stibitz and Jules A. Larrivee, Mathematics and Computers (New York: McGraw Hill), pp. 138-139; Randell, Origins, p. 239.
  41. E. G. Andrews, "A Review of Bell Laboratories Digital Computer Developments," Review of Electronic Digital Computers, Joint AIEE-IRE Computer Conference, December 10-12, 1951, Philadelphia, pp. 101-132.
    Reckoners, Bell Labs, page 0103

  42. Franz Alt, Electronic Digital Computers (New York: Academic Press, 1958), pp. 63ff.
  43. Andrews, "A Review," pp. 103-104; Andrews, "Telephone Switching," p. 348; Stibitz and Larrivee, Mathematics and Computers, p. 148.
  44. Stibitz, text of speech delivered at Hanover, dated September 11, 1940, Stibitz Papers, Box 1.
  45. This theme is discussed at length in Brock, Telecommunications Industry.
  46. Edmund Berkeley, Giant Brains, or Machines that Think (New York: Wiley, 1949), pp. 132-133.
  47. Stibitz, letter to the author, August, 1979.
  48. Martin Mayer, "Computers on the Brain," Esquire, January, 1969, p. 102.
  49. R. W. Hamming, "Error Detecting and Error Correcting Codes," Bell System Technical Journal, 26 (1950), 147-160.
  50. E. G. Andrews, "A Review," p. 103; Andrews, "The Bell Computer, Model Vl," Annals of the Harvard Computation Laboratory, 26 (1949), 20-31.
  51. Berkeley, Giant Brains, p. 143.
  52. Brock, Telecommunications Industry, pp. 191-192.
  53. Ibid., pp. 187-194.


Go Forward, Go Back, Go to Table of Contents, Go to On Line Documents, Go to Go to Antique Computer home page