| Reckoners, ENIAC, page 0104 |
5
Faster, Faster: The ENIAC
Faster, Faster: The ENIAC
| . |
|
| Reckoners, ENIAC, page 0105 |
| Reckoners, ENIAC, page 0106 |
FIRING TABLES
| Reckoners, ENIAC, page 0108 |
| Reckoners, ENIAC, page 0109 |
| Reckoners, ENIAC, page 0110 |
| Reckoners, ENIAC, page 0111 |
BUILDING THE ENIAC
| Reckoners, ENIAC, page 0112 |
| Reckoners, ENIAC, page 0113 |
| Reckoners, ENIAC, page 0114 |

| Reckoners, ENIAC, page 0115 |
| Reckoners, ENIAC, page 0116 |
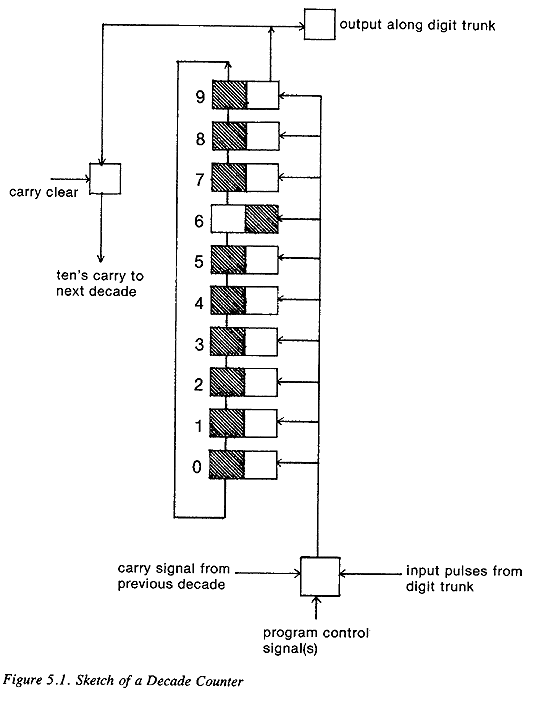
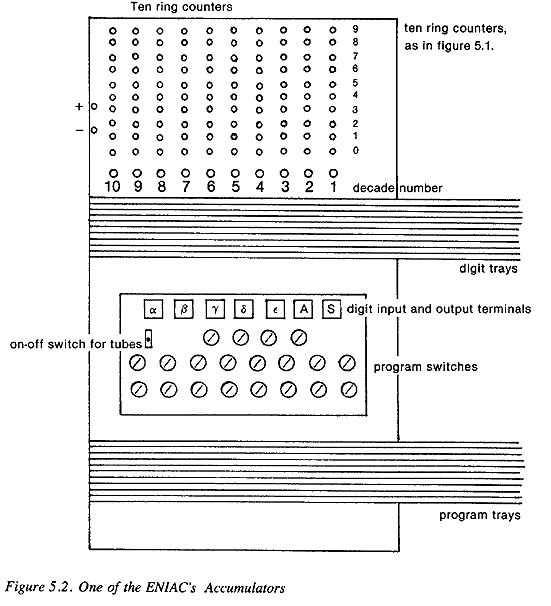
STRUCTURE OF THE ENIAC
| Reckoners, ENIAC, page 0117 |
| Reckoners, ENIAC, page 0118 |
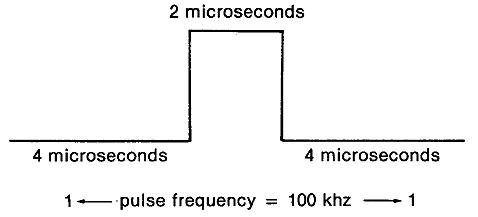
The cycling unit delivered the following trains of pulses: 1) program pulse (1 pulse at the 17th cycle) 2) ten-pulse (10 pulses at the first 10 cycles, shifted a half-cycle in phase) 3) nine-pulse (9 pulses at the first 9 cycles) 4) one-pulse (1 pulse at the first cycle) 5) two-pulse (2 pulses, at the 2nd and 3rd cycles) 6) two'-pulse (2 pulses, at the 4th and 5th cycles) 7) four-pulse (at the 6th, 7th, 8th, and 9th cycles) 8) complement pulse (one pulse at the 10th cycle) 9) carry-clear pulse (one long pulse from the 11th to the 17th cycle) 10) reset-pulse (2 pulses, one at the 13th and one at the 19th cycle).
Figure 5.3. Timing Pulses in the ENIAC
Complex Number Computer, which had a permanently wired program that computed the real and the imaginary parts of a complex product in parallel. (Recall that the Automatic Sequence Controlled Calculator also had a limited parallel capability: to interleave additions between the steps of a multiplication. But it was basically a sequential calculator, as its name implied.)
| Reckoners, ENIAC, page 0119 |
| Reckoners, ENIAC, page 0120 |
| Reckoners, ENIAC, page 0121 |
| Reckoners, ENIAC, page 0122 |
OTHER UNITS: THE MULTIPLIER
THE FUNCTION TABLES AND OTHER UNITS
| Reckoners, ENIAC, page 0123 |
Table 5.1 lists the full specifications for the machine as it existed in 1946.
Table 5.1. THE ENIAC
| Builders: | J. Presper Eckert, John W. Mauchly. Also Arthur Burks, Kite Sharpless, John Davis, Robert Shaw, and others | |
| Place: | Moore School of Electrical Engineering, University of Pennsylvania, Philadelphia. Later moved to the Ballistic Research Laboratory, Aber- deen, Maryland. | |
| Dates: | Proposed April, 1943; authorized June, 1943; completed by November, 1945; first problem run December, 1945. Dedicated February 16, 1946; moved to Aberdeen November, 1946; dismantled October 2, 1955. Parts now in various museums, including the Smithsonian, Washington, D.C., and the Science Museum, London. | |
| Cost: | $500,000 (exactly $486,804.22, according to Goldstine), funded by the Army. | |
| Technology: | Vacuum tubes for computing; electromechanical input and output: card readers, card punches, printers; telephone relay buffer store. | |
| Physical
specifications: | 40 panels, each 9' x 2' x 1', arranged in a U-shape; other units on casters could be positioned at various places. 18,000 tubes, 1,500 relays. 80 different DC voltages, ranging from -920 to + 550 volts; main power 240 volts, 60 Hz. Power consumption: 150 kW, 80 kW for tube heaters, 45 kW for other electronic circuits, 5 kW for input/output devices, 20 kW for ventilating and cooling. | |
| Architecture: | Word length: 10 decimal digits plus sign;
ten's complement for negative
numbers and subtraction; fixed decimal point-switch- selected;
multiplication by table look-up. Addition and subtraction done in
accumulators; separate unit for multiplication, division, and
square-rooting. Other units for cycling (timing), pulse generation, and programming.
| |
| Memory: | 20 numbers in the accumulators: 100 read-only numbers in a function table; other storage by punched cards; also twenty 10-digit constant switches. | |
| Speed: | Pulse frequency, 100 kHz, or one pulse every 10 microseconds. Basic
cycle was one addition time, 20 pulses, or 200 microseconds (5,000 additions/second).
Multiplication time, 14 addition times, or 2,800 microseconds (357 multiplications/second). Division time varied, up to 38 divisions/second. The ENIAC could be run at slower speeds, including a single pulse at a time, or a single cycle at a time, for diagnostic purposes. | |
| Programming: | Plugboards and switch settings. Full conditional branching and subroutine capability; also the ability to perform parallel sequences of operations. Slow to set up: a day or two for each new problem. | |
| Input: | 80-channel IBM punched-card reader; could read 2 numbers/second. | |
| Output: | Standard IBM printer. Each accumulator also had a bank of neon lights showing its contents; at normal speeds these were of course illegible, but at diagnostic speeds they could be read. | |
| Miscellaneous: | Much of the metalwork and other physical construction done by Livingston & Conway, Inc., a Philadelphia construction firm. Cooling system designed and built by Eggly Engineers, also of Philadelphia. RCA of Camden, New Jersey, supplied the tubes. |
EVALUATION OF THE ENIAC
| Reckoners, ENIAC, page 0125 |
| Reckoners, ENIAC, page 0126 |
HOW THE MACHINE WAS USED
| Reckoners, ENIAC, page 0127 |
| Reckoners, ENIAC, page 0128 |
NOTES
- 1. J. Good, "Early Work on Computers at Bletchly," Cryptologiia, 3
(1979), 65-77;
Simon Lavington, Early British Computers (Bedford, Mass.: Digital Press,
1980), Chapters 1, 2.
Reckoners, ENIAC, page 0129
- Cuthbert Hurd, "Early IBM Computers: Edited Testimony," Annals of the
History of
Computing, 3 (1981), 163-182.
- Herman H. Goldstine, The Computer from Pascal to von Neumann (Princeton: Princeton University Press, 1972), Part Two; Nancy Stern, From ENIAC to UNIVAC (Bedford, Mass: Digital Press, 1981); Arthur Burks, "The ENIAC: First General-Purpose Electronic Computer," Annals of the History of Computing, 3 (1981), 310-389.
- John Brainerd, "Genesis of the ENIAC," Technology and Culture, 17 (1976), 482-488; Goldstine, Computer, pp. 127-139.
- Gilbert A. Bliss, Mathematics for Exterior Ballistics (New York, 1944); Edward McShane, John Kelley, and Franklin Reno, Exterior Ballistics (Denver: University of Denver Press, 1953), especially the Appendix on its history, pp. 742-799; Forest Moulton, New Methods in Exterior Ballistics (Chicago: University of Chicago Press, 1926); Thomas J. Hayes, Exterior Ballistics (New York: Wiley, 1938).
- Goldstine, Computer, pp. 146, 137-138.
- Burks, "The ENIAC."
- John Mauchly, "The ENIAC," in N. Metropolis, J. Howlett, and G. -C. Rota, eds., A History of Computing in the Twentieth Century (New York: Academic Press, 1980), pp. 541- 550.
- Nancy Stern, "From ENIAC to UNIVAC: A Case Study in the History of Technology," Dissertation, SUNY, Stony Brook, New York, 1978, pp. 41-48; Goldstine, Computer, p. 150.
- Nancy Stern, "John W. Mauchly: 1907-1980," Annals of the History of Computing, 2 (1980), 100-103; Lewis F. Richardson, Weather Prediction by Numerical Methods (Cambridge, England, 1922).
- Burks, "The ENIAC"; letter from John V. Atanasoff to the author, May 25, 1980; for an example of a special-purpose mechanical device that solved systems of linear equations, see the description of the "Wilbur Equation-solver" in Charles and Ray Eames, A Computer Perspective (Cambridge, Mass.: Harvard), p. 113.
- The Industrial Reorganization Act: Hearings Before the Subcommittee of the Judiciary, U.S. Senate, 93rd Congress, Part 7: The Computer Industry, July 23-26, 1974; Earl R. Larson, Findings of Fact, Conclusions of Law and Order for Judgement, File No. 4-67 Civ. 138, Honeywell, Inc., vs. Sperry Rand Corporation and Illinois Scientific Developments, Inc., U.S. District Court, District of Minnesota, Fourth Division, October 19, 1973.
- H. J. Reich, "Trigger Circuits," Electronics, August, 1939, pp. 14-17; Hurd, "IBM Computers"; W. H. Eccles and F. W. Jordan, "A Trigger Relay Utilising ThreeElement Thermionic Vacuum Tubes," The Radio Review, 1 (1919), 143-146.
- J. Presper Eckert, "The ENIAC," in Metropolis, Howlett, and Rota, A History of Computing, pp. 525-539; Mauchly, "The ENIAC," in Metropolis, Howlett, and Rota, pp. 541- 550; J. Presper Eckert, "A Survey of Digital Computer Memory Systems," Proceedings, IRE, 41 (1953), 1393-1406.
- Arthur Burks, "Computing Circuits of the ENIAC," Proceedings, IRE, 35 (1947), 756- 767.
- Eckert, "Survey of Memory Systems."
- Eckert, "Survey of Memory Systems"; Mauchly, "The ENIAC."
- Burks, "Computing Circuits of the ENIAC"; Burks, "The ENIAC."
- For a popular account of the Colossus, based on interviews with some of the participants, see Christopher Evans, The Micro Millennium (New York, 1980), pp. 34-36. Evans's interviews are available as the "Pioneers of Computing" series from the Science Museum, London.
Reckoners, ENIAC, page 0130
- Burks, "Computing Circuits"; J. G. Brainerd and T. K. Sharpless, "The ENIAC," Electrical Engineering (February, 1948), pp. 163-172; J. P. Eckert, et al., "Electronic Numerical Integrator and Computer," U.S. Patent No. 3,120,606 (June 26, 1947); Herman Goldstine and Adele Goldstine, "The Electronic Numerical Integrator and Computer," Mathematical Tables and Other Aids to Computation, 2 (1946), 97-110.
- D. H. Lehmer, "A History of the Sieve Process," in A History of Computing in the Twentieth Century, N. Metropolis, J. Howlett, and G. -C. Rota, eds. (New York: Academic Press, 1980), pp. 445-456.
- U.S. National Defense Research Committee, Applied Mathematics Panel, "De scription of the ENIAC and Comments on Electronic Computing Machines," Report 171.28, November 30, 1945.
- Franz Alt, "A Bell Laboratories Computing Machine, Part II," in Brian Randell, ed., Origins of Digital Computers, p. 527.
- John Mauchly, "Preparation of Problems for EDVAC-type Machines," in Randell, Origins, p. 366.
- Burks, "Computing Circuits of the ENIAC"; National Defense Research Commit tee, "Description of the ENIAC," p. 3/9; N. Metropolis and W. J. Worlton, "A Trilogy on Errors in the History of Computing," First USA-Japan Computer Conference, October 3-5, 1972 (Tokyo), pp. 683-691; J. P. Eckert, "ENIAC," in Metropolis, Howlett, and Rota, History of Computing.
- For this and the following descriptions of the ENIAC's structure I have relied mostly on Burks, "The ENIAC," cited above.
- National Defense Research Committee, "Description of the ENIAC," pp. 2/4-2/5, also section 4.
- J. Presper Eckert, "Thoughts on the History of Computing," Computer (Decem ber, 1976), pp. 58-65.
- Goldstine, The Computer, p. 145; Brainerd and Sharpless, "The ENIAC," pp. 168-169.
- Industrial Reorganization Act, p. 5810; Eckert, "Survey of Digital Memory," p. 1394.
- Brainerd and Sharpless, "The ENIAC," p. 169.
- Burks, "The ENIAC."
- Nancy Stern, ENIAC to UNIVAC, pp. 62-63; Goldstine, The Computer, p. 234.
- Hartree published several accounts of his experience with the ENIAC: "The ENIAC: An Electronic Computing Machine," Nature, 157 (April 20, 1946), p. 527; and 158 (October 12, 1946), pp. 500-506; a description of the problem he ran on it appears in Calculating Instruments and Machines (Urbana: University of Illinois Press, 1949).
- Herman H. Goldstine, The Computer from Pascal to von Neumann (Princeton: Princeton University Press, 1972), Part Two; Nancy Stern, From ENIAC to UNIVAC (Bedford, Mass: Digital Press, 1981); Arthur Burks, "The ENIAC: First General-Purpose Electronic Computer," Annals of the History of Computing, 3 (1981), 310-389.