Go Forward, Go Back, Go to Table of Contents, Go to On Line Documents, Go to Go to Antique Computer home page

This chapter is revised from an article published in the Annals of the History of Computing ©1981 American Federation of Information Processing Societies.


Reckoners, Germany, page 0010



2
Computers in Germany



.
For about a year now I have been occupied with thoughts about a mechanical brain.
-Konrad Zuse, 19371

In the world of computers Konrad Zuse has not had much influence. There are others, mostly Americans, who had more. But the story of how Zuse came to build a digital computer is not only fascinating in its own right: it can also tell us more about computers than the stories of the others can. Zuse worked independently on his projects, because of the language barrier and because he worked during World War II, when he could not have had any contact with the Americans and the British. That means that his story is almost a laboratory illustration of the major problems in the design and construction of a digital computer, even if the way he solved those problems did not serve as a model for how they would be solved later.

Not only that, but Zuse was the first. He designed and built a working automatic calculating machine by December, 1941, at least a year or two ahead of anyone else.

Konrad Zuse was born on June 22, 1910, in Berlin, where his father was a clerical official with the post office. Shortly after 1910, the family moved to Braunsberg, in East Prussia, where Zuse spent his childhood. (Braunsberg is now the Polish city Braniewo, between Gdansk and the Soviet city Kaliningrad.)2

Zuse has since described the school he attended as being traditional and conservative, with more emphasis on Latin than on other subjects such as mechanical engineering. After a few years there he transferred to a more progressive school in Hoyerswerda (in Silesia, near Dresden), which he enjoyed a bit more. By 1927 he had decided on engineering as a career, and that year he enrolled in the Technical College of Berlin-Charlottenburg.
Reckoners, Germany, page 0011

School records from those years show that Zuse was not especially talented or proficient at mathematics.3 For him, mathematics was a tool with which one could design and build structures, but the structures themselves (buildings, highways, whatever) interested him more. What math he did learn was applied: how to set up and solve equations that described mechanical structures. One particular problem he faced was the analysis of load-bearing structures that are said to be statically indeterminate. If a load is carried by more than two supports one cannot determine how that load is distributed without taking into account the elasticity and strength of the materials involved. Such analysis quickly leads to a system of simultaneous linear equations of sufficient degree to include all those factors. The theory for setting up such equations-for making an analysis of the structures at hand-was already well known by the 1930's. The formulas were in the textbooks.4

The problem was that for all but the simplest sets of equations the tedium of manual calculations necessary to solve them was too great. Doubling the number of equations increases the number of calculations not two-fold, but eight-fold. Engineers did those calculations with the aid of a slide rule, or, if one had the money, a mechanical calculator that could perform arithmetic with greater accuracy. Even with those aids, though, the upper practical limit for an individual is about six equations with six unknowns. Beyond that, the number of elementary arithmetic operations becomes impractical; also, the chances for error in copying and retrieving intermediate results greatly increase. One example from that era was the design of a railroad station; the calculation of the stresses on its roof required the solution of a system of thirty equations in thirty unknowns. Its solution took a team of human computers several months to complete.5

But it was precisely these kinds of problems that the theory of static structures was designed for. It did not matter that the textbooks gave the method of solution, if that solution was so time-consuming it could never be practically carried out. For Konrad Zuse this imbalance between what he found in his textbooks and how the practical world applied those theories led him to the invention of a computer.

The slide rules or mechanical calculators available at the time were capable of performing elementary arithmetic operations one at a time. But even if those operations could be speeded up it would not break the real bottleneck, which was in the routing of those numbers to and from the calculating instruments, writing down and retrieving intermediate results, and gathering the input data at the right time for each stage of the computation. That logistic problem overwhelms the individual problems of computing the sums, products, quotients, and differences of pairs of numbers. It is the complexity of this "traffic control" that grows exponentially as the size of the problem increases, and it cannot be solved by better or faster calculating machines, or by simply hiring more human computers to do the work. Zuse knew little of the existing technology of calculating machines. But as far as mechanizing the logical part of a problem was concerned the calculating machines industry had hardly progressed at all. Circuits that do arithmetic, though they are found at the heart of every modern computer, make up only part of a computer's power.
Reckoners, Germany, page 0012

Zuse's first thoughts about automating this task were to try to represent the problem graphically. He reasoned that for every problem there could be a preprinted form, with labeled boxes into which the input values would be placed. Each graphical location on the form would correspond to a specific arithmetic operation. The user would not have to worry about those operations but would only need to write the numerical data into the appropriately labeled places. Intermediate results would likewise be placed in boxes corresponding to their role in the overall computation. Thus the labeled form would translate the logic of the solution of a system of linear equations into a corresponding graphical layout. The engineer would only have to write down the input values in the appropriate boxes. Someone else-or a machine-could do the elementary operations. In the graphical scheme Zuse envisioned, values that lay next to each other would be multiplied or divided; those that lay under each other would be added or subtracted (see Figure 2.1).6 (Zuse's thinking in graphical terms was to characterize much of his later work in computing, especially his work on programming languages after 1945.)


Reckoners, Germany, page 0013

Once the numbers were in their places, carrying out the arithmetic on them would be so routine that it could be automated. One could link calculators to those specific places--the calculators in turn could carry out the correct operations on the numbers they found there, according to their location on the plane. To avoid copying numbers from the form into a calculator, Zuse thought of entering those numbers in such a way that a machine could take them directly as input-something like a hand-held card punch that could be scanned over the surface of the form, punching in values as needed. From this idea (he had not at this time actually built any apparatus) he thought of having the numbers entered into a mechanical register directly, using push-button switches that hold their position, but which, unlike perforated media, may be cleared for reuse.

At this stage of Zuse's thoughts on how to automate computation, the only step still requiring a human's judgement was the requirement that he determine where on the form (or "solution surface") each number belonged. But why not make that step automatic, too? A person could key numbers into an ordinary keyboard; then an automatic crane would take each number and place it at the correct position on the surface. (The contraption might resemble the treasure-finding cranes found in amusement parks.) The crane would know where to place the numbers because it would be given the x-y coordinates of the surface for each one. It would receive a list of those coordinates beforehand, corresponding to the specific problem being solved (see Figure 2.2).7


Reckoners, Germany, page 0014

To sum up this scheme that Zuse conceived of while a student in Berlin: given a problem in structural engineering, one first translates it into a corresponding mathematical equation or set of equations that will solve it. (This is or should be the most difficult and creative part.) Associated with that particular equation will be a list of x-y coordinates directing the input data to places on a two-dimensional surface. The places correspond to the arithmetic to be performed on each number. Having supplied those coordinates to the machine, the engineer would then key in numbers for the variables in the equation (for example, the length of the span, the weight of the load it is to carry, etc.), and the machine would place them on a surface, where calculators would perform the necessary arithmetic on them.

Now the whole purpose of having the numbers positioned graphically on a surface is to specify what arithmetic operations are to be done on them. But that graphic information is also contained in the coordinates that make up the "plan" of the calculation, so there is really no need to have those numbers represented by a two-dimensional grid after all. The information is redundant. It would be just as easy to connect the individual calculators to the input data via the coordinates themselves, since each one represents a specific arithmetic operation.

What Zuse had discovered, by the back door, was that the plan of a calculation could itself be coded and delivered to a machine-in short, a machine could be programmed to carry out any sequence of simple operations. (Zuse used the word plan, but he understood it in the same way as the modern definition of program.) Such a machine, since it could carry out any finite sequence of elementary arithmetic operations, would be a general purpose computer; it would not be restricted to any one problem or specific type of problem.

Now (c. 1934-1935) Zuse was ready to begin thinking of how actually to construct a machine that would work that way. Figure 2.3 shows the overall design that he sought to implement.

Rather than have separate calculators for each operation as before, he would employ just one calculator (Rechenwerk): one that could perform the four operations of arithmetic. Numbers would be transferred into this calculator from a storage area (Speicherwerk), which could also serve as a temporary storage area for intermediate results. A control device (Programwerk) would direct the transfer of numbers into and out of the store and would also specify the arithmetic operation performed on each number transferred into the calculating unit. The program unit would in turn be directed by a strip of punched tape (Lochstreifen), which contained the overall plan of the calculation.

The design of such a universal calculating machine, which Zuse says he came upon during his student days in Berlin, is not much different from the overall design of a modern computer. In both there is a clear separation of units that perform arithmetic, control, and storage of data. Zuse's design is similar to the first design for a universal computer that was envisioned by Charles Babbage in the 1830's. Babbage never completed his Analytical Engine, but he saw it as being organized around two fundamental units:
Reckoners, Germany, page 0015

First: The Store in which all variables to be operated on, as well as all those quantities which have arisen from the result of other operations, are placed.
Second: The Mill into which the quantities about to be operated on are always brought. 8

Punched cards borrowed from Jacquard's looms were to control the Babbage Engine; perforated paper tape was to control Zuse's.

Zuse was not aware of Babbage's prior work at first, although he did learn of Babbage in 1939, when he tried to obtain a German patent on one of his first mechanical models. (The patent application was rejected.) By that time Zuse felt that he had progressed so far beyond what Babbage had done that he did not stand to gain much from a study of the Englishman's earlier work.9


Reckoners, Germany, page 0016

Zuse graduated from the Technical College in 1935, with a degree in civil engineering, and he began working as a stress analyst for the Henschel Aircraft Company in Berlin. Once there he was faced with the same problem of analyzing indeterminate structures (this time aircraft wings) by solving systems of linear equations. His desire to mechanize the process, first kindled while a student, grew. He began actually constructing a device, turning a portion of the living room of his parents' house on Methfesselstrasse 10 (near the Tempelhof Airport) into a workshop. It was here where his first computers took form.

MECHANICAL CALCULATION, c. 1935

The heart of such a computer would be a calculating machine. How would one build it given the technology of the day? By the 1930's calculators had reached a mature stage of development. (In fact machines of that design continue to be used and sold to the present day.) There were many types available, but they all stored and manipulated numbers by toothed gears or racks, the number of teeth varying from zero to nine according to the decimal digit represented. Mechanical linkages carried a digit from one column to another in the course of an addition (a principle first used by Schickard and Pascal in the early 17th century).10

What differences there were among commercial machines centered around the problem of a carry of 1 from one column to the next (or a corresponding "borrow" of 1 during subtraction). Especially troublesome was the case where a carry propagated itself across several columns, as in the sum

1 + 99999 = 100000.

It was here that the machinery was most likely to jam.

Another difference was in the way the calculators handled multiplication. Most treated it as a repeated addition column by column, building up the partial products step by step. Another method was to compute the partial products directly, just as human beings are taught to do in grade school. The machine is somehow "taught" the multiplication table, using mechanical linkages, metal plates, or whatever, so that it at once generates a complete partial product for each digit of the multiplier.

But just as learning the times table is never easy for most school children, it is mechanically complex to get a machine to know it. So the direct multiplication method was rarely used, even though it was much faster than the method of repeated addition.

These two questions, how to carry digits from column to column, and how to perform multiplication, dominated all discussion of mechanized calculation when Zuse began his work. Others besides Zuse were also thinking of designing fully automatic calculating systems; with few exceptions they all took a mechanical decimal calculator as a starting point, and so these issues were of central concern to them as well.


Reckoners, Germany, page 0017

THE PATH TO THE FIRST COMPUTER

With a degree in civil engineering, Zuse had a command of mechanics and technical drawing, but he knew little of electrical engineering and even less of the principles of mechanical calculators. He was taught the mathematics necessary for his field, but that did not include the recent advances in symbolic logic and set theory that would one day form the heart of computer science. (Germany--especially Gottingen, where David Hilbert taught mathematics--was at the center of those activities.) Zuse's ignorance of calculating machine construction may have been to his benefit; as it turned out, his approach was fresh, original, and not hindered by what experts said could not be done. His ignorance of advanced mathematics may have been a hindrance at first, but it did not remain so long.

The first step he took to implement his ideas turned out to be the most important. That was to abandon the use of mechanical devices which stored numbers by assuming one of ten physical positions, in favor of a simpler system which could assume not ten but only two positions in total. He was thinking of something like a switch that was either on or off, or a lever that was either forward or back.

Thus from the start Zuse was committed to using the binary system of enumeration for his machine. (He never seems to have considered using the decimal or any other base.) He came to the idea not as a mathematician but as a mechanical engineer concerned with keeping the physical apparatus as simple as possible.

The binary system is so central to modern computers that it is hard to realize what a radical and unexpected step it was when first introduced. Our familiar decimal system had been used so long that it was assumed to be almost Godgiven, a stage on which further arithmetic and mathematics was to be played out. Only when someone provided a mathematical analysis of the decimal system, showing that each digit of a number represents a successive power of ten, did the idea occur that one could use other numbers as a basis, including the simplest case of the base two.

As early as 1680 Leibniz worked out the binary number progression and how to perform arithmetic in that base. He mentioned in his writings that it would be possible to mechanize binary arithmetic, but his famous calculator used the ordinary decimal, not binary, system. (Indeed it was such a successful design that it was used as a model for decimal calculators for centuries thereafter.) For his philosophical writings and for his work on binary logic, not for his construction of a decimal calculator, Norbert Wiener called Leibniz "the patron saint of cybernetics."11

Whether or not Zuse got his idea of using binary arithmetic from his knowledge of Leibniz is hard to say. Certainly Leibniz would have been more familiar to a German student than to an Englishman or to an American, but his fame at that time came not from his discovery of binary logic but from his independent discovery of the calculus. Most of his writings on binary arithmetic remained unpublished until recently, when the computer revolution spawned a renewed interest in them. Nor does the fact that Zuse knew of Leibniz's work mean that he would have grasped its significance. A hundred years before, Babbage had studied the works of Leibniz intensively, and had even joined a society at Cambridge devoted to the promotion of Leibniz's work in the calculus. Yet Babbage never considered any but a decimal base for his Analytical and Difference Engines.


Reckoners, Germany, page 0018

One of Zuse's school friends, Walther Buttmann, recalls having searched the library of the University of Berlin (to which he, but not Zuse, had access), for Leibniz's writings on binary arithmetic.12 So we know that Zuse at least was aware of those first halting steps Leibniz took toward a non-decimal number system.

Why was abandoning the decimal system so advantageous? After all, humans learn not binary but decimal numeration, and would certainly shy away from any machine that did not use a base of ten. One obvious advantage is that it is easier to design and construct mechanical elements that assume only two instead of ten positions. That was the main reason Zuse chose the binary system. The problem of machining the computer's parts to a fine tolerance (the problem which undid Babbage's dreams) is much less acute when only two states are needed.

Another advantage, not nearly as obvious, is that yes-or-no elements can also be used to make up the other elements of a computer, especially those that control it. A computer is not just a calculator; it must also direct the course of the calculations it performs. Control devices, which specify what arithmetic operations the calculator performs on a given number, would not at first glance seem to have anything to do with arithmetic devices, and in a decimal computer that is indeed the case. They do different things and they are made out of different basic elements. But the operations of control, when simplified to their most elemental forms, are also two-fold, yes-or-no decisions, and so can be expressed as binary quantities. So with a binary computer the same physical elements can be used: simple two-position levers or switches throughout. It is much easier to visualize and design a machine to carry out an alternating sequence of arithmetic and control operations that make up the process of computing.

Now in such a long sequence, the machine ought to manipulate and transfer numbers from one of its parts to another without any human intervention. The human operator sees the numbers only at the beginning of a computation, when he supplies the input variables, and at the end, when he gets the answer. Those are the times, of course, when the numbers should be in the decimal form. But in a long computation, those two conversions make up only a small fraction of the total computing that the machine does. Intermediate results remain in binary and need not be converted (they are "among their fellows," Zuse said).13

He recognized a fundamental difference between a computer and a calculator: the user of a calculator sees and handles all numbers the machine uses; the user of a computer does not. Converting each number to and from binary is time-consuming, but a computer does not have to do that.

In late 1936 Zuse began building a computer. He worked in the evening in his living-room workshop, after a day's work at Henschel. He enlisted the help of a few friends (Helmut Schreyer, Andreas Grohmann, and Walther Buttmann), who had faith in his idea-even if they did not fully understand what he was doing.14


Reckoners, Germany, page 0019

Their first task was to build a memory device that could accept and store numbers during a calculation. That was actually the simplest part of the machine, since a memory unit only has to represent binary digits without having to provide for the carry of a digit from one place to another. Zuse devised a system in which slots cut in a metal plate stored a number. The position of a pin in each slot represented a binary digit; on one side it was a binary "1", on the other a binary "0". Another plate could be engaged against the pins to sense their position, thereby "reading" the number stored therein, or "writing" numbers into the memory by moving the pins. A third plate, set at right angles to the second, activated the reading and writing functions, by moving the pins to a position where the read/write plate became active (see Figure 2.4).15

Zuse wanted a memory with a fairly large capacity. He decided that the first test device should have an accuracy of sixteen binary digits, corresponding to about four or five decimal digits (less than what ordinary decimal calculators had, but about the same as a slide rule). So he and his friends spent many an evening cutting out the slots in the metal plates-over a thousand were needed.


Reckoners, Germany, page 0020


Reckoners, Germany, page 0021

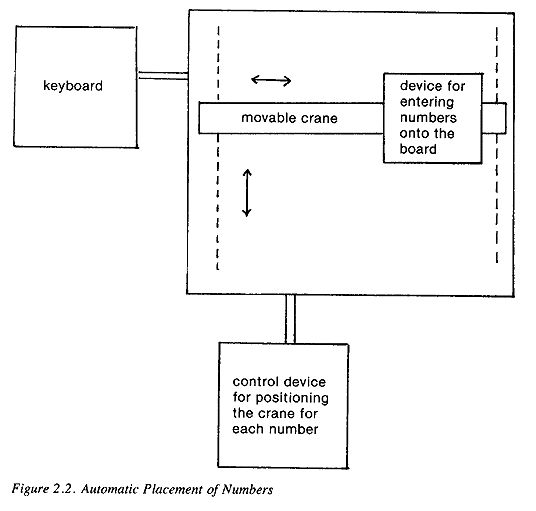
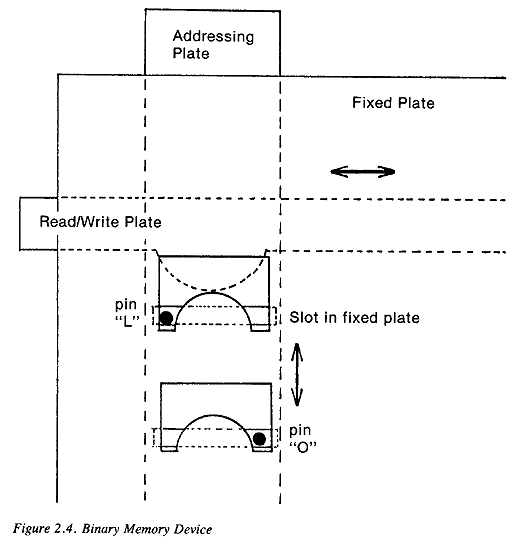
Andreas Grohmann recalls that task, remembering how important was the need to cut the plates accurately:
Kuno [Zuse] drew the form on paper exactly. I pasted the paper on a plywood board, then placed the desired number of plates between it and another board that lay under it. I then screwed the boards together, and sawed out the form of the relays [slots] with a small electric fretsaw. I made these relays by the thousands.16
The memory unit worked. Neither Grohmann nor the others were skilled machinists, and they did not have more than basic hand tools to work with. Their success was due first of all to the modest size of Zuse's machine. But more than that it was due to the simple design that only the binary system can provide.17

Building the arithmetic unit proved to be more difficult. Here it was necessary to link each digit with its two neighbors, in the event of a carry during addition.

One place where the use of binary arithmetic does not simplify matters is the case of a carry propagating itself through a whole number. The addition

1 + 11111 = 100000

is mechanically just as complex as the decimal

1 + 99999 = 100000.

The question of how to implement multiplication, which so baffled calculator manufacturers, interestingly does not come up at all in binary. The binary multiplication table is so simple (1 x 1 = 1; all other products are 0) that it is trivially easy to teach it to a machine. But the price of this simplicity is that the summing of partial products is much more lengthy in binary than in decimal. All multiplication reduces to the addition of partial products.

Zuse has often told the story of how he approached a manufacturer named Kurt Pannke for financial support. Pannke asked what system Zuse's machine used to perform multiplication-table look-up or repeated addition. Zuse told him the two schemes were identical. By using two as a number base he "solved" the problem, as Alexander the Great cut (he did not untie) the Gordian Knot. Pannke was not impressed; he thought that Zuse might be trying to swindle him. But after Zuse explained binary multiplication to him he recognized the principle, and was sufficiently impressed by it to supply much of the money used to build Zuse's first computers.18

There remained the problem of connecting the arithmetic unit to the other parts of the computer. He had already used up all three spatial dimensions for the arithmetic itself; where would he add more linkages to transfer numbers into and out of the arithmetic unit? Whatever he added had to be kept as close to the other elements as possible; at some point the amount of "play" those elements introduced into the system would render it inoperable.
Reckoners, Germany, page 0022

So at that stage of work Zuse began by first making a sketch on paper of the functions and linkages of the arithmetic unit, disregarding for the moment their physical locations in space. He devised a symbolic notation to describe the action of individual two-state mechanical elements, borrowing a notation then in common use to describe electromagnetic relays.

Relays are also fundamentally binary devices, and it would have been possible to build his computer out of them rather than out of mechanical plates. But that was not his reason for using the relay notation, at least not at first. Relays were not cheap, and any computer of adequate size would need thousands of them. They also took up quite a bit of space and would have required a hefty supply of electric power. Besides, Zuse was not as familiar with relays as he was with mechanical devices. He had, after all, already built a reliable and compact mechanical memory.

But just the same, he chose at least the symbolic representation of relays because of its great flexibility. Relay circuits, being linked to one another by wires, do not have to be physically close to one another, as do mechanical linkages.

Using the symbolic notation of a relay, Zuse worked out the basic operations of the arithmetic unit of his computer in terms of elemental yes-no operations. In this way he could set out exactly what he had to build before he began cutting out any metal plates. He called the notation that he developed the "Conditional Combinatoric" (Bedingungskombinatorik) (see Figure 2.5).19

So by 1938 Konrad Zuse had made three fundamental decisions that would characterize his work for the coming decade. The first was his overall plan for the structure of a computer (Figure 2.3). The second was his decision to use the binary system. The third was his development of a symbolic notation by which he could express the machine's functions, especially those of arithmetic and control.


Reckoners, Germany, page 0023

His Conditional Combinatoric combined the rules of binary arithmetic with those for expressing simple logical statements. Zuse referred to the binary states of his calculus not as "one" and "zero," implying only numerical information, or "true" and "false," implying only logical information, but as the letters "L" and "O," implying either. From the standpoint of a mechanical engineer, thinking of levers or relays, there was obviously no difference.

In the Conditional Combinatoric, the expression

(A,B) = > C

would be fulfilled (logically "true," numerically "one") when either A or B was true. The expression

[A,B] = > C

would be fulfilled only when both A and B were true. The expression

-A

would have the opposite value of A, whatever that was. The following expression yields the algebraic sign of the product of two numbers, assuming that the value "true" represents " + " and "false" represents "

[(Lm,Ld), ([Vx,Vy], [-Vx,-Vy])] => Vr

The expression says that the sign (V) of the result (r) is positive for the operations of multiplication (m) or division (d), when either the signs of x and y are both positive or both negative. Note that the result of the operation appears at the right, and is indicated by the arrow formed by typing an equals sign and a greater-than sign. This convention indicates the dynamic aspect of what actually goes on in a machine, and is the opposite of the way mathematical functions are ordinarily written (with the function name at the left and an equals sign joining it to an expression on the right). Zuse's convention avoids confusing equality and the assignment of a value, a confusion that many modern programming languages exhibit. (There was an attempt to have a right-pointing assignment statement in the programming language ALGOL, but it was never adopted. This question will be discussed again in Chapter 6.)20

The conditional chains intended to form the basis for Zuse's computer were the three primitive logical operations: conjunction (the square brackets), disjunction (the parentheses), and negation (the minus sign), corresponding to the logical "and" statement (true only when both statements are true), logical "or" (true when either statement is true), and logical "not" (true when the statement is false, and vice versa). He also combined those primitive statements into a logical equivalence statement, true only when each elemental part of the statement has the same truth value, both true or both false (as in the example of the sign in multiplication).
Reckoners, Germany, page 0024

Mathematicians knew further that chains of these primitive logical statements could express the laws of ordinary arithmetic as well. Since before the turn of the century there had been an effort to show that all mathematics was reducible to a logical basis. As with the discovery of binary arithmetic, that too had its roots in the work of Leibniz. In a remarkable anticipation of the computer age, Leibniz had attempted to construct a universal language, a Lingua Charactera, in which both logical and numerical information could be expressed. But like his exposition of binary arithmetic that idea was all but forgotten by 1935.21

In Germany in the 1930's, Gottingen was the center of efforts to establish a logical foundation for mathematics. There David Hilbert and W. Ackermann led the "formalist" school of mathematics with their Foundations of Theoretical Logic, published in 1928. In the English-speaking world Alfred North Whitehead and Bertrand Russell, in their Principia Mathematica, stated an even bolder "logicist" case.

But Zuse was unaware of those works, including Hilbert's, even though those ideas were at the center of a vigorous debate going on concerning the nature of modern mathematics. When Zuse wrote to his former mathematics teacher, a Professor Naumann, and told him of his "Conditional Combinatoric," Naumann informed him that he had just independently rediscovered what Hilbert had already described as the "Propositional Calculus.22 Naumann further suggested that Zuse study Hilbert and Ackermann's book, which he promptly did, finding in it what would become the theoretical basis for his further efforts to construct a working computer.

So with the help of the Propositional Calculus (nee Conditional Combinatoric), Konrad Zuse could write out the arithmetic and control operations that he wanted his computer to perform, and manipulate those expressions without worrying about how they would be implemented. Only at the final step, after the operations were specified and put into their simplest form, would the "words be made flesh"-put into the form of mechanical pieces that would actually carry out those functions. The mechanical world that he would build would be one generated by mathematical statements-that was a reversal of ordinary applied mathematics, in which the equations described a world already there. Zuse proposed the name "logistic" (as mathematical logic was known in Germany) to describe it; it might well have been called "computer science," which is hardly a better phrase. (In Europe today computer science goes by the name "Informatics.")23

CONSTRUCTION OF THE FIRST COMPUTERS

Now to return to the problem of getting metal plates and levers to obey those logical expressions. With the help of the Propositional Calculus it was possible to simplify expressions to the point where they could be made up of and, or, and not statements. That may not be the shortest or most concise form, but those statements are the easiest to implement mechanically, by a system of interlocking bars (see Figure 2.6).
Reckoners, Germany, page 0025

But despite the aid of the Propositional Calculus, the job proved to be difficult. Zuse completed a small mechanical arithmetic and control unit in 1938 and joined it to the mechanical memory he had constructed the year before. It did not work very well. But it was a start. (Later on, he called that device his "V 1," for the German "Experimental Machine One" [Versuchsmodell 1 ]. After the war he called his machines "Z1," "Z2," etc., to avoid confusion with the V-1 and V-2 rockets that Wernher von Braun had built.)
Reckoners, Germany, page 0026

The V1 worked just well enough to convince Zuse that he was on the right track, but it also convinced him that mechanical computing elements were too difficult to get to work reliably. They were all right for the memory, but for the other units of the computer he began looking for a better method.

Throughout those early days in Zuse's home workshop, he could always rely on the help of Helmut Schreyer, a college mate, a student of electrical engineering, and a handsome amateur actor of considerable charm. Schreyer was one of those who helped cut out all the metal plates for the Z1. While a student Schreyer had worked as a film projectionist-he and Zuse were especially fond of the sensational American film King Kong, then just released in Germany. He remembered that in a movie projector, the film advances through a gate where each frame is stopped for a moment so that it can be projected on the screen.

That was precisely the kind of motion the programming unit of Zuse's computer needed-a quick reading of the calculating plan, one command at a time. From then on Zuse designed his computers to have their programs supplied by perforated movie film instead of paper tape. (Discarded 35mm film was cheaper than commercial paper tape anyway.)24

From Schreyer's training as an electrical engineer came a conviction that electrical computing elements could be made to work much better than Zuse's mechanical elements. Schreyer had a confidence and familiarity with telephone relays that Zuse did not have. Telephone relays were not that expensive-a few dollars each-but remember, thousands would be required. Nevertheless he convinced Zuse to adopt them. They managed to find very cheap second-hand telephone relays and they rebuilt them to work in a computer.

Zuse had already been using the relay notation as a design aid, so the transition was not hard to make. In 1938 and 1939 Zuse pressed on with that approach: a mechanical memory, an arithmetic and control unit made of relays, and program control by perforated 35mm movie film.

Schreyer went one step further. Why not build the binary functions out of vacuum tube circuits? Up until that time tubes were used to amplify continuous signals, but he knew he could build a tube circuit that would have the same on-or-off properties that relays and mechanical linkages have. Such a "tube relay," as he called it, would switch by moving streams of electrons and would be many times faster than any electromechanical relay.

By that time Zuse was convinced that his chances of success with telephone relays were too good to pass up. There was a lot of developmental work needed to perfect the "tube relay" circuit, which he was not willing to undertake. Schreyer in turn suggested to Professor Stablein at the Berlin Technical College that an investigation of the electronic switching circuit be the subject of his doctoral thesis. Stdblein agreed, and in 1941 Schreyer was awarded a doctoral degree for his thesis, "The Tube Relay and the Techniques of its Switching." Figures 2.7 and 2.8 show two of the circuits that Schreyer built.25
Reckoners, Germany, page 0027


Reckoners, Germany, page 0028

The key to their operation was the use of a gas-filled lamp which conducted only after a certain threshold of voltage was passed; but once conducting, it would continue to conduct with a lower "holding" voltage flowing through it. (The familiar fluorescent light is such a lamp; it requires a "starter" to turn it on.) This threshold effect gives the circuit two well-defined states, analogous to the open and closed positions of a relay and quite unlike the continuous output of an ordinary vacuum-tube circuit.

While Konrad Zuse was going ahead with a calculating unit that used telephone relays, Schreyer proposed to build one out of vacuum tubes, using, of course, Zuse's overall design and the binary scale. He managed to obtain special tubes well suited for his circuits from the Telefunken Company. But when he submitted his proposal for a full-scale computer to the German Army Command (OKH) in 1942, he was turned down. At that time, the German authorities thought the war would be over within the two or three years Schreyer knew it would take to complete the machine. And they did not want to fund anything that would not directly benefit the waging of the war. The proposed machine was to have about 1,500 tubes, and as many glow-lamps.26

The story of Schreyer's attempt to build an electronic computer in Germany during the war is one of the more interesting "what-ifs" of that entire period. By 1942 he was working independently of Zuse, and had his proposal been accepted, Germany might have had a working electronic computer before either the Americans or the British. It was true that his circuits were not as fast, nor was his proposed machine as large as the American ENIAC, but with his use of Zuse's elegant overall design, and especially with his use of the binary system, he might have come up with a very powerful computer.

So for a moment, then, Schreyer cracked open the door to an awesome and strange new world, but that door slammed shut before he could pass through. Only after the war did a now-divided Germany enter the electronic computer age, but as a follower, not a leader.

All that Schreyer built was a test model containing about 150 tubes that converted three-digit decimal numbers to and from binary. (It was financed not by the army but by the Aerodynamics Research Institute.) It was damaged in a bombing attack on Berlin in late 1943, and with Schreyer's evacuation from Berlin in 1945, Germany's first steps toward electronic computing came to an end. After the war Schreyer left Germany and abandoned work on computers. (Konrad Zuse was not a member of the Nazi Party, but Helmut Schreyer was: he had joined in 1933. After the war he emigrated to Rio de Janeiro, where he worked for Brazil's telecommunications network, and where he still lives.)27


Reckoners, Germany, page 0029

Schreyer has since reflected on what might have been. The American ENIAC project was given a go-ahead in the middle of the war, and its builders were given all the manpower and money they needed to see it through (not without some difficulty, as we shall see). They did not complete their machine until after the war was over either. But by that time no one really cared that it was late--there were other jobs it could do. Getting a machine running in time to help the war effort would have been an issue for the Germans, who were losing badly after 1943. Schreyer was never able to assemble a team of qualified helpers, and this, coupled with the lack of money, killed the chances for success. In this regard Zuse made the right choice to stay with second-hand telephone relays, since he could get by with more modest resources. Zuse had already faced the same problems convincing the German authorities of the importance of his work; in the fall of 1939 he was drafted into the infantry and sent to the front, but was soon recalled to work as an aircraft engineer.

Schreyer wrote a letter to the German authorities to help get Zuse back to Berlin. The letter describes the potential benefits of Zuse's computer work, and, incidentally, is one of the earliest known documents describing the operation and programming of an automatic computer.28

Zuse built a small binary arithmetic unit out of second-hand telephone relays, joining it to the mechanical memory of his "VI." The results were encouraging enough to convince him that a full-scale computer could be built along those lines and would work well. He approached the Aerodynamics Research Institute (DVL) for help. They were not interested in a general-purpose computer, but they did have a computational problem which, as they said, "was burning their fingertips," it was so urgent. That was the wing-flutter problem, one which Zuse had already encountered while at the Henschel plant. At certain high speeds the wings of a plane would resonate-flutter like a flag in the wind. To prevent their failure one had to design the wings so that their resonant frequency was higher than the speeds the plane would ever encounter in flight. Airplane wings are not "static" structures, but the analysis of their resonance can be done by treating the wing like a static indeterminate structure such as a bridge or a roof. In both cases the analysis requires the solution of large systems of linear equations. For an airplane wing the coefficients are complex numbers, taking into account the phase of the pressure waves of air across it.29

Zuse invited Alfred Teichmann of the DVL to his parents' apartment to have a look at his machine (now called the "V2"). It ran well enough to impress Teichmann (Zuse claims it never worked again!), and so the DVL agreed to help finance a completely new machine. Before building it Zuse decided to build one more "provisonal" test machine-this one using telephone relays for both memory and for arithmetic-one which would incorporate all the features of his original design for a general-purpose programmable computer. He still relied mostly on his own funds and still worked in his home workshop, but with the encouragement of the DVL, he proceeded at once to build a relay computer that functioned reliably in every respect. It was completed by December, 1941, and was the first fully operational program-controlled computing machine in the world. It is now known as the Z3 computer.30


Reckoners, Germany, page 0030

DESCRIPTION OF THE Z3

Like Schreyer's electronic circuits, the Z3 did not survive the war. It was destroyed in a bombing raid on Zuse's workshop in 1945. What little we can find out about that historic machine must be gleaned from the patent applications he filed for it, and from personal recollections from those who saw it in use. In 1961 a replica of the Z3 was reconstructed for the German Museum of Technology, in Munich, and although it is not an exact copy, it does give a good idea of what the original Z3 must have looked like.31

The reconstructed Z3 reveals three large units: two relay cabinets, and a keyboard/display panel. Just to the right of the keyboard is the device that read in programs from perforated movie film. The original had two racks of relays for the storage of sixty-four numbers, not just one rack, as the replica has. Each memory cabinet was six feet high and three feet wide. On the whole the Z3 was a modest machine, nothing like some of the "giant brains" that later would be built in America.

The size of the cabinets that held the Z3's memory reveals why Zuse was reluctant to abandon a mechanical approach. He knew that a full-scale computer having sufficient power to do useful work would need far more than sixty-four memory cells-a thousand was a more realistic requirement. But to store 1,024 numbers (as he planned for his next machine) using relays would have required thirty-two cabinets like the one used for the Z3's memory. That would have taken up a lot of room and needed a lot of power. Zuse returned to a mechanical store for his Z4, which eventually stored 512 numbers in a very compact and reliable unit. He never seriously considered building a computer on the huge scale of the ENIAC or the Harvard Mark I.

All computing and storage in the Z3 was done with ordinary telephone relays, although their contacts were carefully adjusted so that their opening and closing times were all within a specific range. This was necessary to synchronize the running of the whole system.

These telephone relays are two-position switches, open or closed. Telephone networks also use other relays, which have more than two positions. (In all but the newest telephone networks, rotary-dial phones make a connection by activating such multi-position relay switches.) The Z3 also used eight of these "uniselectors," as the telephone company called them; they were mounted in the enclosed area at the bottom of the right-hand relay cabinet. These switches controlled some of the detailed sub-operations of multiplication, division, and taking the square root; addition and subtraction were handled entirely by binary relays.

The Z3 had a total of about 2,600 relays: 1,800 for the memory, 600 for the arithmetic, and 200 for the film reader, keyboard, and display. Assuming that the relays cost about two dollars apiece, then Zuse must have spent about fifty-two hundred dollars for relays alone. Other materials costs may have added another thousand dollars. There were also labor costs, although Zuse and his friends donated hours and hours of their time. Considering the materials alone the Z3 probably cost between six and seven thousand dollars, a figure that agrees with estimates Zuse gave to the DVL. (He said that he had spent around twenty-five thousand Reich Marks for the machine.)32 That is a lot less than the cost of any other comparable device built in those years.
Reckoners, Germany, page 0031

The relays were purchased second-hand, cleaned, and synchronized with one another. They required 60 volts DC, supplied synchronously to all parts of the computer by a rotating drum mounted below the arithmetic cabinet. Each rotation of the drum directed one full operation of the computer, such as the storage of a number into a memory cell.

The drum could be spun at varying speeds, up to a limit of five cycles per second (300 RPM). It could be slowed down to a single step at a time, useful if someone wanted to trace a computation step by step.33

The drum controlling the flow of current through the machine was set up so that current was sent to the relays only after they had switched. This so-called current-free (stromlos) method of switching prevented arcing at the relay contacts, and so made the machine more reliable. (When any large currents are switched, arcing can occur at the moment of switching, when the connection is only partially made. By having all current switched at the rotating drum, any contact wear is now shifted to the carbon brushes on the drum, and these are inexpensive and easy to replace.)

That principle made the Zuse computers extraordinarily reliable-they could run for months without needing repairs. Telephone relays are simple devices not prone to failure, but to use them in a computer requires more reliability than a telephone system needs. Unlike in a telephone system, the relays in a computer must work every time; furthermore those relays go through more cycles in just one hour of computing than they might in a week of telephone use.34

A DETAILED LOOK AT THE Z3

Figure 2.9 shows the calculator-style keyboard and display panel of the Z3 replica. Numbers were keyed in by pressing the appropriate buttons on the lower panel; results were read from the upper panel, which contained small incandescent light bulbs for each decimal digit. In both input and output the numbers were represented in their floating-point, decimal form, with the decimal point assumed to be after the first digit in the first column, and the power of ten indicated by a row of buttons or lamps along the bottom of each panel. The Z3 had a decimal accuracy of four decimal places, with a range of 10±9 (answers could range farther, to 10±12).

The keyboard also had buttons for the four ordinary operations of arithmetic, plus square root, divide or multiply by ten, divide or multiply by two, and multiply by -1. (Some of these functions were not built into the replica.) When a number was keyed into the machine, it was converted into its floating-point, binary form before being stored or used for a calculation. On the replica this binary number was indicated by a set of twenty-two lights on the arithmetic relay rack.
Reckoners, Germany, page 0032


Reckoners, Germany, page 0033


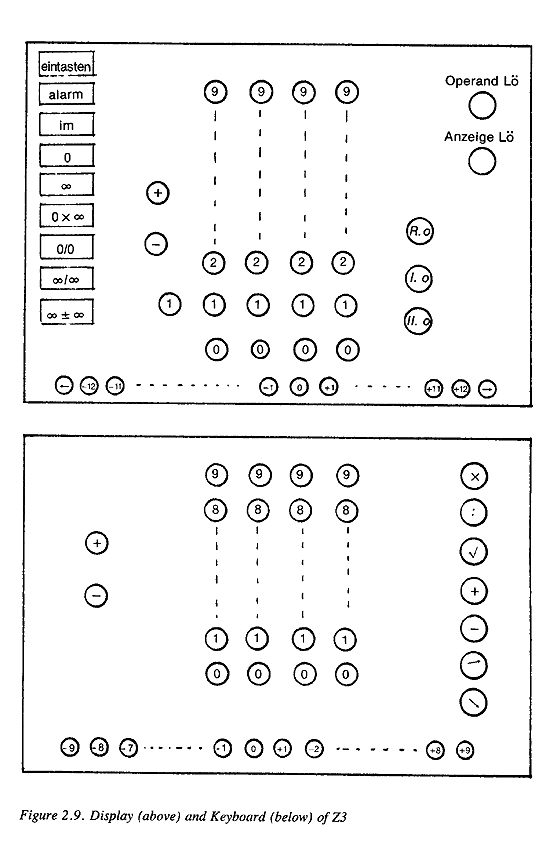
Reckoners, Germany, page 0034

Additional lights on the display panel were for special results. Lights at either end of the exponent field indicated when the results overflowed or underflowed the machine's capacity. If the machine was told to take the square root of a negative number, the display "im" for "imaginary" would light up. (The Z3 did not automatically handle complex numbers, although of course one could write a program to do that. Since the analysis of the flutter problem involves matrices that have one or more complex elements, it was likely that Zuse eventually wanted his computers to handle those numbers).

There was also a special light for true zero, since in floating-point arithmetic, true zero cannot otherwise be represented (0.000 x 10° may mean a number as large as 0.0005).

If division by zero occurred during a computation, a special display for "infinity" would light up. Similar displays indicated indeterminate results such as "infinity" x 0, 0 / 0, or "infinity" / "infinity". In certain cases these quantities would factor out of a computation, so their presence would not necessarily mean a wrong answer. This feature has been implemented in several modern computers, including the CDC 6600, but it has not become universally adopted.35

Programs were read into the Z3 by a simple device that sensed the presence of holes in a strip of film. A hole stood for the binary value "1" or "+"; no hole for "0" or "-." The film was prepared by a simple manual punch having eight buttons, one for each channel of the filmstrip. The holes were staggered slightly to prevent tearing. For example, the number LOOLLLLO would be punched into the film as follows: 

       L O O L
        L L L O

The film sensing device was built in Darmstadt with the help of Alwin Walther and W. de Beauclair, two of continental Europe's other computer pioneers.

Table 2.1 summarizes the specifications of the Z3. 

Table 2.1. THE Z3


Technology: electromagnetic relays: 2600 binary: memory            1400
                                                 arithmetic         600
                                                 misc.              600
                                       20 step switches
Number System: floating-point binary
	word length: 22 binary digits:              sign             1 bit
                                                  exponent         7 bits
                                                   mantissa       14 bits
Memory Capacity: 64 numbers
                  random access
Input/Output: push-button keyboard, display by incandescent bulbs, 
              one for each decimal digit
Programming: eight-channel perforated filmstrip, basic commands of + , - , 
              x ,	- , square root, shift binary or decimal point
		"zero-addressing" (see text)	

	
  Reckoners, Germany,   page 0035 	


Dates:	completed 1941, destroyed 1945; 
             replica built after original plans, 1963, 
             now in German Museum, Munich
Place: Berlin, Methfesselstrasse 7 (near Tempelhof Airport)
Cost: 25,000 RM, or about $6,500
Speed:        3-5 seconds/multiplication
              clock frequency: 4-5 cycles/second

A person keyed floating-point decimal numbers into the Z3. It converted them into floating-point binary. The twenty-two relays that held a number were divided as follows:
the first seven relays held the power of two,
the next relay the algebraic sign of the number,
and the remaining fourteen relays the mantissa of the number.
In floating-point binary the first digit of the mantissa is always "1" (just as in floating-point decimal the first digit is never zero), so that "1" was not stored. The decimal number 398, for example, would be stored as: 
       398 = 110,001,110 in binary
           = 1.1000111 x 101000 in floating-point binary
or, using Zuse's notation:

      000L000     L      L000LLL0000000
      -------     ^      -----------------
      exponent    |      mantissa (with leading L dropped)
		sign digit (+ )
Representing numbers by floating-point binary in the Z3 was its most interesting feature; it was something no other functional computer would have for years. As an engineer, Konrad Zuse recognized from the start that such a representation was better suited to the kinds of problems he faced, but to get a machine to handle numbers that way was not a simple task. Floating-point arithmetic has an additional effect of making the operation of addition slower (since the exponent has to be adjusted before the mantissae can be added to each other), while it makes multiplication a little faster (since one obtains the exponent of a product simply by adding the exponents of the two operands). In engineering calculations, multiplication occurs more frequently than it does in business or accounting work, so on the whole the Z3 was a more balanced machine given the kind of work it was designed to do.

Zuse called his representation "semi-logarithmic form," since the exponent may be thought of as the characteristic of the logarithm of the number.

PROGRAMMING THE Z3

Programming the Z3 is best illustrated by looking at the problems it was designed to solve, namely the evaluation of the determinant of a matrix. For the matrix
Reckoners, Germany, page 0036 

         | a  b  c |
         | d  e  f |
         | g  h  i |
the determinant is given by the following formula:

Det = (aei + bfg + cdh) - (ceg + bdi + afh)

To evaluate that expression using only pencil, paper, and slide rule, a person would perform the multiplications, additions, and subtractions as they appear in the formula above, writing down intermediate results along the way. (It is also possible to rearrange the expression slightly to minimize the number of intermediate results that has to be recorded.)

Programming the Z3 to compute the determinant was similar. A film strip having the same sequence of operations coded into it would be fed into the machine. The initial values would be placed manually into memory cells, and other memory cells would be used to store intermediate results for later use. The program would connect the calculating unit of the machine to the correct memory cells for each step of the problem.

The calculating unit did all the arithmetic; the memory unit only stored numbers. If the result of one calculation was needed for the very next calculation, there was no need to store it in the memory only to retrieve it immediately. In that case the number remained in the register of the calculating unit where it was needed anyway. Only numbers needed more than once or needed at some later step had to be stored in memory.

For an operation like multiplying two numbers together, the program would recall both numbers from memory and place them into registers in the calculating unit before it gave the command to multiply. Today this is known as "postfix" notation, in contrast to the more familiar "infix" notation of placing the operation between the two operands. Postfix notation is also found today in some pocket calculators, where it goes by the name of "reverse Polish" notation (after a Polish logician named Jan Lukasiewiecz, who first proposed it for writing logical expressions in the 1920's). Zuse's machine was probably the first to employ postfix notation-his Z3 not only specified operations after the operands, it also contained circuits in its calculating unit that ensured that the operands were in the proper order for division and subtraction.36

The D3's arithmetic instruction set assumed that the operands were already in place in the calculating unit. In modern terms the Z3 had a "zero-address" coding scheme, since no memory address needed to be specified for an operation. (A sample Z3 program-and the same program for a modern calculator that uses postfix notation-is found in the Appendix, in section 1.)


Reckoners, Germany, page 0037

It was not difficult to produce a coded filmstrip for a problem once the mathematical expression was given. So while only Zuse himself could service the machine, he hired others to program it. Because of the manpower shortages during the war, he wrote to an institute for the blind in Marburg and requested a list of blind people who were gifted in mathematics. From this list he hired August Fast to produce programs. Fast learned the job easily and so became one of Europe's first computer programmers.37

The Z3 was designed to test the feasibility of a machine that would solve the flutter problem for the Henschel Company. It passed that test. But it was also a general-purpose machine that could be programmed to solve other problems just as well, since the solution of the flutter problem was similar to the solutions of many other similar ones.

In Germany during the 1930's, H. G. Kussner had worked out a mathematical analysis of the wing-flutter problem by developing an iterative procedure whereby the determinant of a matrix (whose elements were complex numbers) was computed for successive values of approximate forces on a wing. When the determinant becomes zero, Kussner showed that the elements of the matrix equalled the actual forces on the wing. This method computed those forces without having to build a wing and test it in a wind-tunnel, which was the only other way to get that information.38

So the method required computing determinants, each time with slightly different matrix elements. In a 1941 report, Alfred Teichmann (who had seen Zuse's V2), compared the numerical method with the wind-tunnel method, saying, "A disadvantage of carrying out the flutter calculations is the huge expenditure of effort which it requires: 100-400 man-hours to calculate a simplified system."39 Teichmann did not mention computers in that report, but he obviously saw the advantages of having a machine take over the job.

The Z3 was never put into routine use for that or any other problem. But it did run a number of test programs and did so reliably and without error. Several people visited Zuse in his home workshop and observed it in operation. Dr. Alwin Walther, H. J. Dreyer, and W. de Beauclair of the Institute for Applied Mathematics in Darmstadt saw it during a visit to Berlin, and of that visit de Beauclair has said: "On the ground floor of the house we saw it. It demonstrated for us the solution of a determinant. We were very much impressed; we probably never had even thought of this approach-binary, relays, punched tape control."40 Dreyer remembers the machine as a series of racks on which the relays were mounted, there being a clear separation of units for memory, arithmetic, control, input, and output. He says further:
The Z3 was fully functional. For a series of different calculations there were program tapes available, for example for systems of linear equations. One could key in the coefficients, and the results were displayed. From my recollection it ran without error.41


Reckoners, Germany, page 0038

That it was never put into routine use was due to its limited memory, which meant that it could not compute the determinant of large matrices where manual methods were impractical.

Such is the story of the Z3. It lived for about four years and never performed routine useful work, but it stood at the gateway to the computer age nonetheless. How significant was it? The modern computer owes far more to the American and British wartime machines than it does to the Z3. Indeed, its very existence was hardly known to historians or computer scientists until the 1960's.

None of that detracts from what the Z3 was: possibly the first machine to be programmable in a general way, to use the binary system, to use floating-point arithmetic, and to have an elegant logical design.

Actually the Z3 was only one part of the German contribution to computing; besides the prototype electronic circuits that Helmut Schreyer built during the war, there were several other relay machines that Zuse constructed which are also part of the story.

The Z3 was only a test machine, but Konrad Zuse also built a relay device that was put to practical use by the Henschel Company during the war. That was the so-called Sl; a machine that carried out a fixed sequence of operations that Zuse permanently wired into its circuits.

The S1 was smaller than the Z3, using about 800 binary and 30 multi-position relays. It too worked in the binary system (fixed point), and had a memory of six cells. The fixed program it carried out was a sequence of sums of products. The computation aided the production of the Henschel HS-293, an unmanned flying bomb that was carried aloft by a bomber and then released and guided remotely to its target. 42

In normal aircraft production, the wing and rudder surfaces must be machined accurately. But for an unmanned flying bomb that would have been too expensive. Instead, the wings were fabricated cheaply, with the understanding that there would be inaccuracies. These inaccuracies would be measured, and then the S 1 would calculate how far the bomb would deviate from a straight path because of them. The wings and rudder could then be adjusted along a movable axis to compensate for the error, but no expensive refabrication would be necessary. The S1 took a set of about 100 measurements of the wing and calculated the resulting aerodynamic performance. When it was put into service at Henschel, it replaced a team of thirty to thirty-five women who worked with desk calculators. Human "computers" were a dying breed.

The flying bomb was successfully produced and deployed in large numbers toward the end of the war, especially against Allied shipping in the Mediterranean after August, 1943. It was also used in the German retreat from Poland in 1945. It made a modest contribution to the German war effort.43

Zuse built one other computing machine during the war that ranks with the Z3 as a pioneering computing device. That was the Z4, a full-scale relay machine that he started to build as soon as the Z3 demonstrated the feasibility of the overall design.


Reckoners, Germany, page 0039

The Z4 (or V4, as it was known then) was to have been the full-scale general purpose computer the DVL wanted for aircraft design. Its construction was begun in 1942, and it used the same design as the Z3, with a few differences.

One difference was that it was to have a longer word length-thirty-two binary digits instead of the Z3's twenty-two. This gave it an equivalent of seven decimal places, with a range of 1020 for both input and output.

But the main difference was its much larger memory: Zuse planned a capacity of up to 1,024 numbers, although that was not achieved. For that memory Zuse returned to a mechanical memory device, like the one he first built for his "V1" four years before. So the Z4 would have a memory unit that was about a third the size of one of the Z3's relay memory racks, yet it would have many times the memory. (Eventually a 512-cell store was built, having eight times the capacity of the Z3.) That capacity was far greater than anything being designed in America or England at the time.

Designing the Z4 was straightforward, but its construction was severely hampered by Allied bombing raids on Berlin after 1944. Zuse had to move it three times to different parts of Berlin; at least once he was moving it even as the building was being hit. (In one of those raids, on April 6, 1945, the Z3 was completely destroyed.)44

The Z4 was finally moved out of Berlin in early 1945, first to Gottingen (where it performed test computations), then to an underground fortification in the Harz Mountains, then to a village in the Bavarian Alps. There it stayed during the chaotic postwar years, until it was finally refurbished and put to work at the Federal Technical Institute in Zurich in 1950.45 For a few years it was the only functional computer, electromechanical or otherwise, in continental Europe, and it initiated much of Europe's postwar activity in computing thereafter.

So despite incredible hardships and hard luck, the work of Konrad Zuse, Helmut Schreyer, and their co-workers was not totally lost. The Z4's influence was modest, but the machine worked well and was heavily used at Zurich, even after the computing world had turned from relay machines to the faster electronic technology. During his stay in Hinterstein, the Alpine village where the Z4 rested from 1945 to 1949, Konrad Zuse did not abandon work on computing. Work on the Z4 itself was impossible: even getting enough to eat was difficult in those years, and Zuse lacked the tools and manpower to do much more than just try and save what he had. He turned his attention to the problem of programming computers-pencil-and-paper work that few at the time thought was crucial to making use of a computer's power. Today the cost of writing programs for computers far exceeds the cost of the machinery itself. Now that the computing world faces this "software crisis," it should be remembered that here, too, Konrad Zuse made original contributions. His work on a "Plan calculus," begun in 1945, was one of the first attempts to design a programming language for a computer.46


Reckoners, Germany, page 0040

After the Z4 was installed in Zurich in 1950, Zuse founded a private firm that made and sold relay machines to industrial and educational customers. For the Leitz Optical works he built a relay machine that he called the Z5, and after that he built a series of other relay computers, the last being the Z11, built in the mid-1950's. His company also built electronic computers, and for a while it prospered. In the 1960's it had trouble raising capital and was absorbed into the Siemens company. That left Konrad Zuse free once again to pursue the theoretical side of computing. He is still active, a remarkable feat in a field that is so volatile and fast-developing.47

So what do we have in the story of the first computers in Germany? They are not the ancestors of the modern computer; that honor goes elsewhere. But their overall design and their use of binary numbers and floating-point arithmetic make them resemble the modern computer far more than an ancestor like the ENIAC does. The German story is a fascinating one, and it has a lesson for us as well. The key concepts of computing were discovered independently in different places by different persons. That the present computer world bears the imprint of the American projects was not inevitable; things could have turned out very differently.



NOTES

  1. Konrad Zuse, Der Computer, Mein Lebenswerk (Munich: Verlag Moderne Industrie, 1970) p. 68.
  2. Zuse, Der Computer, pp. 15-16; C. Evans, interview with Zuse, "Pioneers of Computing Series" (London: Science Museum, 1976).
  3. Notebook 17, Zuse Archives, Gesellschaft fur Mathematik and Datenverarbeitung, Bonn.
  4. Konrad Zuse, interview with the author, April, 1978.
  5. Wilfred de Beauclair, Rechnen mit Maschinen (Braunschweig: Vieweg, 1968), p. 2.
  6. For a discussion of the symbolic analysis of Zuse's graphical scheme, see F. L. Bauer, Between Zuse and Rutishauser-the Early Development of Digital Computing in Central Europe, Technical University, Munich, Department of Informatics, Report 7629 (Munich, 1976).
  7. Zuse, Der Computer, pp. 36-39.
  8. Charles Babbage, "Passages from the Life of a Philosopher," in Charles Babbage and His Calculating Machines, ed. Philip and Emily Morrison (New York: Dover, 1961), p. 55.
  9. N. Metropolis and J. Worlton, "A Trilogy on Errors in the History of Computing," Annals of the History of Computing, 2 (1980): 49-59.
  10. De Beauclair, Rechnen mit Maschinen, pp. 11-15; W. Meyer zur Capellan, Mathematische Instrumente, 2nd ed. (Leipzig, 1949), pp. 53-55; Friedrich A. Willars, Mathematische Instrumente (Berlin, 1926), pp. 28, 48-51.
  11. Anton Glaser, History of Binary and Other Nondecimal Numeration (Southhampton, Pa., 1971); Hans J. Zacher, Die Hauptschriften der Dyadik von G. W. Leibniz, ein Beitrag zur Geschichte des Binaeren Zahlensystems (Frankfurt am Main, 1973), pp. 18-34; "Hewn von Leibniz' Rechnung mit Null and Eins," transcription of MS, 1679 (Munich: Siemens A. G., 1966).
  12. Quoted in Karl-Heinz Czauderna, "Konrad Zuse-der Weg zu seinem Computer Z3 and dessen Verwircklichung," Report 120, Gesellschaft fur Mathematik and Datenverarbeitung (Bonn, 1979), pp. 88-89.
    Reckoners, Germany, page 0041

  13. Konrad Zuse, "Method for Automatic Execution of Calculations with the Aid of Computers," German Patent Application Z 23 139 IX/42m, April 11, 1936, reprinted in Brian Randell, ed., The Origins of Digital Computers: Selected Papers, 2nd ed. (New York: Springer Verlag, 1973), pp. 159-166.
  14. Czaudema, "Konrad Zuse," pp. 85-89.
  15. Ibid., pp. 31-40.
  16. Ibid., p. 89.
  17. E. Jessen, "Konrad Zuse-Konstructeur der ersten programmgesteuerten Rechenanlage," paper presented at the Advanced Course on General Net Theory of Processes and Systems, Hamburg, Oct. 10, 1979.
  18. Zuse, Der Computer, pp. 75-76; also Zuse Archiv, Bonn, # 009/002.
  19. Zuse, Der Computer, pp. 53, 64.
  20. F. L. Bauer, Between Zuse and Rutishauser, p. 36; see also the discussion by Bauer on the history of ALGOL, Association for Computing Machinery (ACM) SIGPLAN Notices 13, no. 8 (August, 1978), p. 40.
  21. Morris Kline, Mathematical Thought from Ancient to Modern Times (New York: Oxford, 1972), chapter 51; Jean van Heijenoort, From Frege to Godel: A Source Book in Mathematical Logic (Cambridge, Mass.: Harvard, 1967), introduction.
  22. Zuse, interview with the author, April, 1978.
  23. Konrad Zuse, "Ober Programmgesteuerte Rechenanlage fur industrielle Verwendung," Probleme der Entwicklung programmgesteuerte Rechengerdte and Integrieranlage, ed. H. Cremer (Aachen, 1953), p. 74; Konrad Zuse, "Die ersten programmgesteuerten Relaisrechenmaschine," 350 Jahre Rechenmaschine, ed. M. Graef (Munich, 1973), p. 55.
  24. Helmut Schreyer, "Die Entwicklung des Versuchsmodells einer elektronischen Rechenmaschine," unpublished, Mosbach/Baden, Aug. 1, 1977.
  25. Helmut Schreyer, "Das Rohrenrelais and seine Schaltungstechnik," dissertation, Technische Hochschule, Berlin, August, 1941.
  26. Ibid., p. 77.
  27. Records of party membership were obtained through the Berlin Document Center, Mission of the United States.
  28. Schreyer's letter has been translated and published in Brian Randell, Origins, pp. 167-169.
  29. Alfred Teichmann, "Das Flattern von Trag- and Leitwerken," Deutsche Akademie der Luftfahrtforschung, Schriften 49 (1941); Zuse, interview with the author, April, 1978.
  30. A letter from the DVL to Zuse, April 22, 1942, Zuse Archiv No. 014/008, states that the "provisory" machine (that is, the Z3) was completed by December 5, 1941.
  31. German Patent Application Z-391, applied for in 1941, rejected May 7, 1956; letter from de Beauclair to Czauderna, in Czaudema, "Konrad Zuse," p. 98; letter from Dreyer to the author, July 23, 1978; letter from Zuse, Zuse Archiv, No. 014/001.
  32. Zuse, Der Computer, p. 82; correspondence between Zuse and DVL, Zuse Archiv, No. 014/008; interview with Zuse by Uta Merzbach, Zuse Archiv, No. 030/002.
  33. Czaudema, "Konrad Zuse," pp. 70-73; Wend Goldbach and Rolf Schneider, "Beschreibung der Rechenanlage Z3," Zuse Forum, 2 (September, 1963), 19-31.
  34. H. Flessner, private communication, October 10, 1979.
  35. See, for example, John Ball, Algorithms for RPN Calculators (New York: Wiley, 1978), p. 163; Donald E. Knuth, Seminumerical Algorithms (Reading, Mass.: Addison Wesley, 1969), pp. 192-193, 205.
    Reckoners, Germany, page 0042

  36. Ball, Algorithms, chapter 1; John Kennedy, "RPN History," paper presented at the Western Calculator Conference, Anaheim, Calif., Sept. 22, 1979.
  37. Zuse, Der Computer, pp. 83-84, 93-94; Zuse Archiv, No. 017/013.
  38. H. G. Kussner, "Flugelschwingungen an Flugzeugen," Zeitschrift fur Angewandte Mathematik and Mechanik, 9 (1929), 492-493; H. G. Kussner, "Zusammenfassender Bericht uber den instationaren Auftrieb," Luftfahrtforschung, 13 (1936), 410-429.
  39. Alfred Teichmann, "Das Flattern"; letter from DVL to Zuse, May 6, 1943, Zuse Archiv, No. 028/008; Konrad Zuse, "Some Remarks on the History of Computing in Germany," paper presented at the Conference on the History of Computing, Los Alamos, New Mexico, 1976; C. Evans, interview with Zuse, "Pioneers of Computing" series.
  40. Letter from de Beauclair to Czaudema, in Czauderna, "Konrad Zuse," p. 98.
  41. Letter from Dreyer to the author, July 23, 1978.
  42. Interrogation summary of Gerhard Overhoff by U.S. Forces in Austria, Air Interrogation Unit, 8 Nov., 1946, p. 1; correspondence in Zuse Archiv, Nos. 028/009 and 036/012.
  43. Rowland F. Pocock, German Guided Missiles of the Second World War (New York: Arco, 1967), pp. 33, 44-45.
  44. Zuse, Der Computer, pp. 87-90, 97, 106; correspondence in the Zuse Archiv, Nos. 002/004, 014/001, 017/009.
  45. R. C. Lyndon, "The Zuse Computer," Mathematical Tables and Other Aids to Computation, 2 (1947), 355-359; "Applied Mathematical Research in Germany, with Particular Reference to Naval Applications," British Intelligence Objectives Subcommittee (BIOS), Report No. 79, pp. 63-64; "The Development of Theoretical and Applied Mechanics in German Institutions During the War," Great Britain, Field Information Agency, Technical (FIAT), Final Report No. 1167, 1947.
  46. F. L. Bauer and H. Wossner, "The Plankalkhl of Konrad Zuse: A Forerunner of Today's Programming Languages," Communications ACM, 15 (1972), 678-685; Donald E. Knuth and L. T. Pardo, "The Early Development of Programming Languages," Encyclopedia of Computer Science and Technology, ed. Jack Belzer, vol. 7 (New York: Dekker, 1977).
  47. See, for example, Konrad Zuse, "The Emancipation of Data Processing," paper presented at the Advanced Course on General Net Theory of Processes and Systems, Hamburg, October, 1979.


Go Forward, Go Back, Go to Table of Contents, Go to On Line Documents, Go to Go to Antique Computer home page