Reckoners Chapter 3

Go Forward, Go Back, Go to Table of Contents, Go to On Line Documents, Go to Go to Antique Computer home page

Reckoners, ASCC, page 0043

3
Bessie ---
The Automatic Sequence
Controlled Calculator

.

... if it should ever turn out that the basic logics of a machine designed for the numerical solution of differential equations coincide with the logics of a machine intended to make bills for a department store, I would regard this as the most amazing coincidence that I have ever encountered.
-Howard Aiken, 1956¹

In the summer of 1944, the American press reported the waging of the war: grim news of battles in France, casualties, sacrifices and shortages at home. Among the stories on August 7 was another report that probably did not arouse much attention. On that day a large electromechanical computing machine was publicly unveiled at Harvard University, in a ceremony attended by the presidents of both Harvard and the IBM Corporation. The machine they dedicated that day was called the ASCC, short for Automatic Sequence Controlled Calculator; later it would be known as the Harvard Mark I as other similar devices appeared there. It was not really the first automatic computer. Zuse's Z3 was already in use by then, and there were other top-secret projects in America and Britain that also could have vied for that claim. But nonetheless its dedication is as good a moment as any to mark the beginning of the computer age, for it was on that summer day that the existence of the computer became public knowledge.²

The Mark I was well publicized, and the details of its construction were duly reported in the press. It was a general-purpose calculator that could carry out a sequence of operations specified by a program punched in a paper tape. It was not a test machine like the Zuse computer but a full-scale device that was put to work as soon as it was completed (well before its dedication that summer). The public dedication brought news of computing machines to a world still at war, while it also marked the entry of both the IBM Corporation and Harvard University into the business of building and using large- scale digital computers.

Reckoners, ASCC, page 0044

Like Konrad Zuse's relay computers, the Mark I was the product of the vision and hard work of one man, although its enormous size and scale required the cooperation of a large team of skilled collaborators. That man was Howard H. Aiken, Commander in the U.S. Naval Reserve and Professor of Applied Mathematics at Harvard.

Aiken grew up in Indianapolis, Indiana, where he attended the Arsenal Technical High School. He went on to the University of Wisconsin, where he received a B.S. in 1923, and then he worked as a power engineer for the next twelve years. But he returned to school as a doctoral candidate in physics, first at the University of Chicago and then at Harvard, where he submitted a thesis on "The Theory of Space Charge Conduction" in 1939.

He got interested in automatic calculating machinery while working on that thesis. Like Zuse, he found himself spending hours computing sequences of sums and products, aided only by a desk calculator and some scratch paper. What was worse, for many of the problems he was trying to solve (involving the numerical solution of differential equations) he found that the sheer number of individual calculations rendered any solution impossible. He just could not do them all in a reasonable time without making errors. It was not for any theoretical reason concerning the numerical methods themselves.
NUMERICAL METHODS OF SOLUTION

The problems that stumped him were nonlinear differential equations which only numerical methods could solve. To solve those kinds of equations required evaluating an integral: finding the area that would lie under the curve of an equation if it were plotted on graph paper. For many equations one can find a corresponding formula that gives the area directly. They are called analytical solutions; for example, the area under the curve described by

y = sin(x), between two points, x1 and x2,
is given by the formula

A = cos(x2) - cos (x1)

But for many equations, especially those of the complexity that Aiken faced, it is not possible to find such an equation. The area must be found by breaking it up into small rectangular "slivers," whose height and width are known. (The person selects the width in advance; the height of each sliver is given by plugging the appropriate value into the original equation.)

So evaluating an integral by such numerical methods is straightforward; it is the sum of the areas of each individual narrow sliver, whose areas are in turn found by a simple multiplication of a constant width by a varying height.

Reckoners, ASCC, page 0045

The difficulty with numerical methods lies in the need to divide the area under the curve into a large number of narrow slices to ensure enough accuracy in the answer. Mathematicians had long ago established guidelines for just how fine this mesh had to be for a given type of integral, but the logistics of carrying out those elementary sums of products became a severe bottleneck as Aiken worked on his thesis: not just the calculations themselves but the writing down, labeling, and accurate recopying of intermediate answers mushroomed to unmanageable proportions.⁴

Aiken saw no reason why the whole process could not be carried out by machinery: specifically by suitable combinations of commercial accounting and tabulating equipment. Especially if intermediate results could be punched into cards rather than written down, the errors of copying and reentering numbers would be reduced.

The first element of the system would be a card reader that would supply the values of the function to be integrated. (Someone would have to punch the cards, but by the 1930's many tables of mathematical functions were already being supplied as decks of punched cards in addition to the more familiar form of books of printed tables.) The values of the function would be taken from the card reader to a multiplying punch, where the area of each sliver would be computed and punched onto another deck of cards. This deck would be taken to an accumulating punch that would sum up the areas, and punch the results onto cards. Finally those cards would be fed into a printer that would print the results automatically.

In this method of computing, each part of the whole sequence of operations is performed for all the values of the independent variable before the deck of cards is transferred to the next station: first the values of f(x) are supplied, then all the multiplications are done, then all the additions, and so on. Intermediate results take the form of decks of punched cards that are physically carried (by hand) from one station to another.

But Aiken felt that the intermediate steps of punching cards should also be eliminated. Why not connect the various machines to one another by wires and not use cards or printing except for the first and last steps? But to do that would require a change in the way the computations were carried out. Instead of doing first all the multiplications, then all the additions, and so on, the machines would have to do the entire sequence of calculations for each value of the independent variable: for each x, find f(x), then find the area of the narrow segment under the curve at f(x), then add that value to the sum of the areas obtained thus far. The machine would have to perform sequences of elementary calculations, in contrast to the parallel method suggested by the way that existing machinery operated.

Reckoners, ASCC, page 0046

(Consider evaluating f(x) = x³ + 3x² + 4x + 4, for x = 1, 2, 3, . . . ,10. Using punched card equipment, a multiplier would first be set up to produce the cubes of the x's: 1, 8, 27,..., 1000, punched into a deck of cards. Another multiplier would be set up to produce the next term: 3, 12, 27, . . . , 300, and so on. Finally the decks of cards representing the values of those terms for all values of x would be fed into an accumulating punch, which would sum their values to produce and punch the list of values of f(x) on a deck of cards. That deck could be fed into a printer if desired. By contrast, a sequential calculator would compute f(x) by performing the individual operations for each value of x, one at a time: f(1) = 12, f(2) = 32, . . . , f(10) = 1344. Hence the name "Automatic Sequence Controlled Calculator" that he gave to his project.)

In 1937, while still a graduate student, he wrote a proposal for such a machine.⁵ This proposal began by summarizing the reasons such a machine with its novel way of computing sequentially was needed, and the various attempts that had been made in the past to construct such a device. It discussed in particular the unsuccessful attempt by Charles Babbage a century earlier to build an Analytical Engine-a machine Aiken recognized as a genuine ancestor to his proposed sequence calculator.

Most of his proposal dealt with how the calculator differed from the punched card machinery of the day. The major difference was of course that the devices for addition, multiplication, reading cards, and punching or printing results would each be connected to one another and would sequentially carry out a computation. (Aiken called the method computing in "lines" instead of "columns," thinking of how a numerical solution would be arranged on a page.)

Other features his machine would have were the ability to handle positive and negative numbers equally well; an ability to supply, automatically, tables of commonly used functions such as sines, cosines, logarithms, and probability functions; and the ability to automatically increment the value of the independent variable each time a sequence is carried out.

That last requirement is useful for numerical integration, where the width of each rectangle is a small constant. There is no reason why the machine should not supply those values automatically once it has been given a starting value and the size of the constant increment. Implicit in that requirement is the need for the machine to stop incrementing the x-value when it reaches the endpoint of the integration.

The remainder of the proposal describes how a general-purpose sequential calculator could be built out of only a few basic components: out of machines that could perform the four basic arithmetic operations, that could read selected values of functions from punched cards or tape, and that could store and retrieve intermediate results on mechanical registers.

The picture painted by Aiken's 1937 proposal is one of equipment racks on which are mounted individual subassemblies-the innards--of standard business equipment. Each of these assemblies would be connected to the others by a switchboard of wires. Other equipment would supply constants such as pi or e, or specific constants pertaining to a given computation. A standard printing device would print the results directly, thus avoiding copying errors.

The sequence of operations would be controlled by punched cards or by a long punched tape, as well as by physically wiring the individual units to one another through a plugboard. That was the way that Babbage wanted to control the operation of his Analytical Engine-borrowing the idea from the silk-weaving industry, where by the 1830's punched cards were widely used to control the pattern woven into the cloth. (The idea is usually attributed to J. M. Jacquard, who successfully employed the method in his looms in Lyon in 1805; cruder versions had been known in France since the 1720's.)

Reckoners, ASCC, page 0047

So Aiken proposed to use perforated media for both numerical storage (as business machines used cards), and for control (as Jacquard looms used them), in a single machine. The idea was a novel one (actually it originated with Babbage, but it was not picked up again until Aiken's proposal). The business machines industry had developed the use of punched cards from the work of Herman Hollerith, who first applied them for the U.S. Census of 1890. But Hollerith was probably not influenced by either Jacquard or Babbage, and the industry that grew up around his invention never used the cards for anything but data storage. Whatever control those machines had was done by plugboards. It was left to Howard Aiken to see what had been clear to Babbage but strangely had been neglected since: that punched card equipment could not only calculate: it could also direct the sequence of those calculations automatically, using perforated cards or tape for each.

To ensure enough accuracy of the results of any calculations done on such a calculator, Aiken proposed that the machine be able to handle numbers of up to twenty-three decimal places in its individual registers. That was over twice what commercial business equipment handled, but Aiken recognized a fundamental difference in the kinds of problems his machine would be solving. Business calculations are carried out to dollars and cents: two and only two digits to the right of the decimal point. Few businesses dealt with amounts of money in the range of millions of dollars, so seven or eight decimal places to the left of the decimal point were almost always more than adequate. Business equipment and desk calculators therefore had a capacity of eight to ten decimal digits, with the decimal point fixed two places from the right of the register.

But scientific calculations could range throughout the number fields, positive and negative, with very small quantities just as likely to occur as very large ones. Zuse had met that problem by adopting floating-point arithmetic, with part of each number set aside to store the position of the radix point. But that complicated the construction of his machines; it would have been intolerably complex had he not taken advantage of the simplicity of the binary scale of enumeration.

Reckoners, ASCC, page 0048

But Aiken was committed to modifying commercial business equipment, which operated in the decimal system and had a fixed decimal point. So he proposed a register that could hold twenty-three decimal digits, with the decimal point fixed at the middle, giving a decimal range of at least 10^±. The breakdown of the digits was to be:
0 000 000 000 000 . 000 000 000 00 ^ ^ ^ | | | sign decimal point two "guard digits" that would be rounded 0 = + , 9 = - off in the final answer

So Aiken retained the simplicity of registers with a fixed decimal point while giving them a much longer "word length" to allow his machine to handle quantities more typical of scientific calculations.

If Aiken drew the inspiration for his proposed automatic machine from Charles Babbage's Analytical Engine a hundred years earlier, he also knew that Babbage never completed more than fragments of that Engine.⁶ Babbage was known to some in the 1930's not as a man of great vision but rather as a failure: an impossible, irascible dreamer who could not anchor his dreams in the reality of iron, brass, and steam. Aiken felt that Babbage's "principles were theoretically sound," but he felt that the problem lay in the Englishman's having to rely on a machine-tool industry which was not up to the demands of the project. The Analytical Engine was to have been powered by a steam engine. Today that seems faintly ludicrous; if he had been successful, would we see today's computer designer doing his business with an oilcan and an adjustable wrench instead of with a voltmeter and an oscilloscope? But Babbage had no alternative to steam: in 1830 electricity was still a mysterious force, and practical motors that harnessed it were still half a century away. Aiken of course could draw on the experience of forty years of business machines and commercial calculators (both industries were established after 1890), but he still had to face skepticism from his peers. His proposed machine was much more complicated than the business machines he was to build it out of. There certainly was the risk that he would fail, just as Babbage had failed, in getting all those individual pieces to fit and work together as a system.

But Aiken succeeded. The Mark I was completed only a few years after he proposed building it in 1937. Whatever else may be said about its design, it worked. It succeeded where Babbage had failed, and its dedication in 1944 served as an existence theorem for the large-scale digital computer. (By 1944 there was at least one other large-scale computing machine that had been built that was the Differential Analyzer which was built under the direction of Vannevar Bush at MIT. But it was an analog, not a digital computer, and so its existence did not resolve the question of whether or not Babbage's century-old dream of a general-purpose large-scale digital computer would ever be more than just that-a dream).

Aiken first sought assistance from the Monroe Calculating Machine Company to build the computer. But they turned him down. The Harvard astronomer Harlow Shapley suggested to Aiken that he go to the IBM Corporation. Shapley knew that Professor T. H. Brown of the Harvard Business School was on good terms with President Thomas Watson of IBM. Through Brown, Aiken was introduced to Watson. So began not only Harvard's but also IBM's involvement in computers.⁷

Reckoners, ASCC, page 0049

Watson had already begun exploring the use of his company's computers for scientific applications, with the establishment of a Computing Bureau at Columbia University (under Wallace Eckert) in 1934. He did not believe that scientific work would ever displace the more mundane business data processing as IBM's bread and butter. But he was sufficiently impressed by Aiken's proposal to commit his company's resources to the building of the calculator, although most of the money used for its construction came from the U.S. Navy.⁸ What IBM contributed most was the experience and skill of a veteran team of engineers from its Endicott, New York, plant, where its punched card equipment was designed and built. The senior engineer put in charge of the project was James W. Bryce, who had been with the company over thirty years; during that time he amassed a long string of patents covering many aspects of the company's line of punched card equipment. Bryce in turn assigned Clair D. Lake, Frank E. Hamilton, and Benjamin M. Durfee to the project at the Endicott plant. Aiken's own role was not as an engineer, even though he had experience in engineering. It was rather as a consultant to IBM's own engineers: Aiken would sketch out what he wanted the machine to do; Hamilton, Lake, and Durfee would match those needs with what they knew existing IBM machinery could do. Aiken spent the summers of 1941 and 1942 in Endicott, but in the early years of the war he also entered active duty as a commander in the Navy, stationed at the Navy School of Mines in Virginia. At least some of that time was spent performing duties entirely unrelated to computers. Nevertheless, Aiken seems to have fitted himself well into that role; he was a self-disciplined man who wore his Navy uniform well. And though he had very specific ideas about how his computer would function, he was glad to be able to use the resources of IBM and that company's engineers to realize those objectives. Unlike Konrad Zuse, Aiken did not immerse himself in the details of building the components of the machine.⁹

The Automatic Sequence Controlled Calculator was completed by January, 1943, in Endicott, where it secretly demonstrated its abilities. It was then disassembled and moved to Cambridge, to a room specially prepared for it in the basement of Harvard's Cruft Laboratory (a few years later the Harvard Computation Laboratory-and the Mark I-got their own building). It began doing serious work for the Navy's Bureau of Ships in May, 1944, three months before its public dedication.

Before that unveiling, the ASCC was covered with a polished stainless steel and glass enclosure: not an easy matter given the wartime shortages of those materials. Watson insisted on it, although Aiken preferred leaving the case off to make the computer easier to maintain and modify. Watson's decision reflected his attitude toward the project and the IBM Corporations's general approach to computing machinery.¹⁰ He did not see much future in making scientific computers, but that is not to say that in the 1940's IBM was content to provide machines that only did simple tabulating and counting. In fact, IBM had already developed machines that had quite a capability for advanced numerical processing by 1944.

Reckoners, ASCC, page 0050

A decade earlier the company had designed and marketed an electromechanical multiplier, the Type 601, that accepted two eight-digit decimal numbers

Reckoners, ASCC, page 0051

punched into a card and computed and punched their product in the remaining columns of the card. (What was interesting about the 601 was that it computed products not by repeated addition, as most mechanical calculators did, but rather by looking up an internally stored multiplication table for the 10 x 10 decimal digits.) By the late 1940's they were working on replacing the electromechanical parts of the 601 with vacuum-tube circuits that could operate much faster. In 1942, under the direction of R. L. Palmer, they had developed a prototype "cross-footing" punch that multiplied electronically.¹¹ Work on electronic computing circuits continued at a separate lab in New York City; after 1945, research and development of electronic devices was centered at a laboratory in Poughkeepsie, New York. (Endicott remained a center for electromechanical research and development.) When IBM unveiled their Type 603 Multiplier in 1946, it was one of the first commercial devices anywhere that calculated with electronic circuits. (The 603 could perform up to sixty multiplications per second, which was about a hundred times faster than the 601. )

Now a suitable combination of IBM's commercial equipment, including the 601 multiplier, coupled with tabulating, card reading, and printing machines, could certainly do some scientific calculations just as easily as Aiken's Sequence Controlled Calculator. Indeed, Wallace Eckert had been using those machines at Columbia for astronomical calculations with great success (where, among other things, he calculated the orbit of the moon).¹² These standard punched card machines that IBM produced could be programmed to do short sequences of arithmetic, using plugboards to determine which operations would be performed on selected fields of the punched cards. What they could not do was execute an arbitrarily long sequence of operations, the kind Aiken wanted his proposed machine to do. But of course that was precisely the point-the Mark I's completely flexible programming made it a general-purpose computer-not just a fancier calculator, but something qualitatively different. The engineers and executives at IBM, and elsewhere too for that matter, did not see that distinction as clearly in 1944 as it is seen today.

So while IBM engineers took on building the ASCC, they did so because of its status as a military project, not as a potential prototype for a future line of commercial products. The U.S. Navy supplied most of the estimated $300,000 construction cost of the machine, with IBM providing additional money for maintenance and support. The total cost was probably over a million dollars; hardly in the same range as the rental costs of IBM's existing lines of business equipment.¹³

The gulf between Aiken's and Watson's perception of the future of computing was hardly evident at the dedication ceremony, but it was deep. In accepting the machine from Watson, Aiken and President Conant of Harvard graciously acknowledged their debt to Watson and IBM, but although Aiken would go on to build other large scale computers at Harvard, he did so without IBM's help. And for the company that was to dominate the computer industry after 1955, the Mark I was really a reluctant step into a new world.

Reckoners, ASCC, page 0052

DESCRIPTION OF THE MARK I
The public dedication of the Mark I in 1944 brought a wide response from other mathematicians and engineers, who saw in it a way to solve problems they too were facing. So in contrast to other wartime projects that were kept strictly classified, the Harvard Computation Laboratory felt the need to provide a detailed description of the Mark I and how it was programmed. Only the specific military problems for which it was first used remained secret. Of course any publicity about the machine would also reflect upon the expertise of the IBM Corporation, even if they were not offering that kind of product to their customers.

The staff of the Computation Laboratory prepared a detailed Manual of Operation for the Automatic Sequence Controlled Calculator in 1946, listing Aiken and Lieutenant Grace Murray Hopper as principal authors. It is from that manual that we can get a detailed picture of how the machine worked and what it could do.¹⁴ The Manual describes the machine as it existed on September 1, 1945; after the war it was fitted with a so-called Subsidiary Sequence Mechanism, which extended its powers, but by that time it was already fast becoming obsolete.

The fundamental calculating element of the Mark I was a wheel that could assume one of ten positions, for the ten decimal digits, just like a desk calculator. (Some wheels had up to twenty positions: ten decimal digits, and others for control, carry, and transmission of numbers from one wheel to another.) A mechanical desk calculator indicates numbers by digits printed on the wheels themselves, but that was not the case with the Mark I. It stored and counted numbers mechanically, but it transmitted and read those numbers electrically. A wiper attached to each wheel made contact with one of ten wires, one for each decimal digit, and that indicated the wheel's position. And the wheels were turned not by a mechanical linkage but by an electric motor that advanced the wheel to a position that corresponded to the number it was supposed to represent.¹⁵ Hence the description of the Mark I as an electromechanical computer.

In a desk calculator, number wheels are engaged by their contact with the keys that the operator presses. If the operator keys the number 6 in a certain column, the wheel corresponding to that column will move six and only six additional places from its initial position (it may also initiate a carry if the wheel passes through zero). In a mechanical device first the keys are pressed, then the number is "loaded" onto the wheels by pulling a lever that moves each wheel the appropriate number of places.

In the Mark I that transfer was accomplished electrically, by a clutch attached to each wheel. A 5-hp electric motor drove a long shaft that ran the full fifty-foot length of the machine. When, say, the number 6 was to be loaded onto a wheel, the clutch would couple that wheel to the shaft for a precise interval of time, until the wheel had moved the six places. Then the clutch would disconnect the wheel from the shaft (see Figure 3.1).

Reckoners, ASCC, page 0053

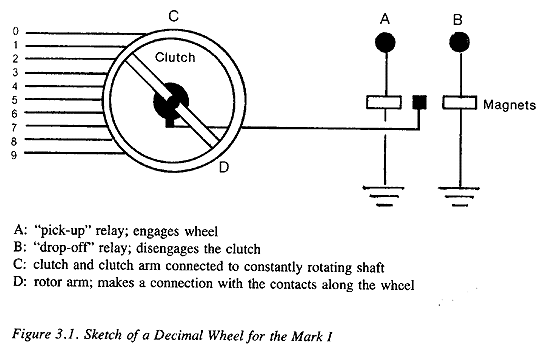
The timing pulses for the clutch relays were supplied by a series of cams connected to the same rotating shaft. The cams could have up to twenty lobes
depending on their function. To add the number 6 to a register, an electrical signal would be routed through a six-lobed cam, which would pick up the clutch on the wheel for six units of time before dropping it off, while also keeping track of any carry digit produced.

Should a number be subtracted from an accumulator (as the cells were called), an electrical signal was sent to another cam having the "complement" of the number's lobes (the difference between the number and nine: for example, the complement of six is three). The shaft and the wheels always turned in the same direction, but by adding the complements of numbers, with an appropriate carry adjustment, the machine could subtract any number from an accumulator. (An explanation of subtraction by complements is given in Glossary B.)

Note that when a number is added to a wheel, that wheel passes through all the digits in between its original position and the sum. If the wheel was at the position for number 3, and the number 6 was added to it, it would be connected to the motor for six units of time, during which the wheel would pass through the positions 3, 4, 5, 6, 7, 8, and 9, where it would come to rest. That is the way all mechanical calculators work (at least all that use decimal numbers). When human beings perform addition they usually proceed directly to the sum of two digits, previously having memorized the addition table. Occasionally a person forgets that table and has to add the numbers unit-by-unit on his fingers. (From the Latin word for finger comes the word digital itself. A digital machine, whether it be a computer or anything else, operates with discrete units.)

Reckoners, ASCC, page 0054

For that reason the storage cells of the Mark I were called accumulators, since they accumulated numbers in them one unit at a time. An accumulator further- more does not distinguish between storing a number and adding a number; when a number was transmitted to a cell of the Mark I, it was automatically added to whatever quantity was already in that cell from a previous operation. That property follows from the way electrical impulses advanced its counting wheels. (Also, any carry digits produced must be transmitted from one column to another; the cells of the Mark I, built from pieces of standard punched card equipment, had that ability as well.) Simply to store a number in an accumulator required that it be set to zero beforehand; that was done by subtracting whatever number was in it from itself just before instructing the accumulator to accept a new number for storage.

Modern terminology is often not as strict about preserving this distinction between an accumulator and a register, which is the name given to a memory cell that simply writes over any number in that cell when a new number is sent to it. Computers today use binary arithmetic; their design favors doing all arithmetic in a central processor (as the Zuse machines did). With few exceptions, modern memory units can store but not accumulate sums; hence the term register to describe them. The main difference between those registers and the "accumulators" also found in the processors of modern computers is that the former do not contain carry circuits. But nowadays that distinction is not strictly adhered to. Aiken often referred to the accumulators of the Mark I as registers, when they were being used only for storage of a number. (Both terms should be further distinguished from a counter, which can also accumulate sums, but which can only be fed numbers from its right-most column.

An automobile odometer is a counter; miles are added to it only a tenth of a mile at a time. An accumulator can add quantities to any column. These terms are further explained in Glossary B.)

The fact that addition (and subtraction) was done in the accumulators had an important bearing on the overall architecture of the machine. The Mark I had no real "central processor" like the Zuse computers or like most modern computers. Any memory cell could be used for addition and subtraction-and there were seventy-two such cells. Only multiplication and division were done in a separate processor unit. That design reflects the Mark I's legacy: punched card accounting equipment that was mainly used to tabulate and accumulate totals.

The Mark I's seventy-two accumulators could perform addition and subtraction, as well as ordinary storage, by first clearing their contents to zero. Accumulator number 71 (they were numbered from 1 to 72) was constructed so that it could be split in half to handle two twelve-digit numbers. Transferring the contents of the other accumulators through it allowed the machine to store twice as many numbers, each having half the precision. Aiken noted that trade-off was useful for statistical problems "where the quantities dealt with are large in number and of low accuracy."¹⁶ That such a feature was built into the Mark I suggests that the twenty-three digit word length was probably too long for many applications, meaning that the full capacity of the accumulators often was wasted. But at the same time, the Mark I also had the ability to link accumulators 68 and 69 to each other, giving the machine a double precision of forty-six digits plus sign. The need for that kind of numerical precision arose in one type of work that the Mark I was especially designed to do-to compute and print tables of mathematical functions to many decimal places of accuracy.

Reckoners, ASCC, page 0055

Accumulator 72 was fitted with another special circuit that gave it interesting properties. I have already mentioned that the Mark I performed subtraction by adding complements-by adding the difference between the subtrahend and 999999. . . , then adding the digit 1 (the so-called end-around carry) to the unit's place, viz.:
45793 45793 -15342 +84657 the 9's complement of 15342 ------ ------ 30451 130450 + 1 the end-around carry; the 1 at ------ the left-most column drops 30451 away
But if the result of a subtraction is a negative number, there is no end-around carry produced at the left-most column. What happens instead is that the digit 9 (which stood for - in the Mark 1) would appear in the sign-field, followed by the complement of the true answer:
5793 5793 -15342 +84657 complement of 15342 ------ ----- -9549 90450 last four digits are the complement of the difference = 9549 sign digit = 9 no end-around carry
Accumulator 72 could detect when no end-around carry took place, and then it would stop the machine. In that way, a function could be evaluated by repeated iterations; after each cycle the value would be tested against a tolerance value stored in cell 72. When the numerical accuracy of the Mark I exceeded that tolerance, the machine would stop, "knowing" that further evaluation of the function would not increase the accuracy of the result.¹⁷

Thus the Mark I could automatically direct the course of its sequence of calculations, at least in this limited way. The question of whether or not the early computers could "choose" their paths of computation is a controversial one, central to the distinction between what a computer is and what it is not, even today. The Mark I had that capability, if only in a limited sense: it could sense the results of its previous calculations and act on that knowledge (that is, stop if programmed to do so by its operator). What it could not do was go to a different sequence of operations depending on the number in cell 72. That capability, which is really what is meant by the term conditional branching as it is applied to computers, was only added to the Mark I after 1945 (as it was added to Zuse's Z4 computer when it was installed in Zurich after 1949).

Reckoners, ASCC, page 0056

Aiken does not seem to have recognized the importance of that kind of logical decision making beyond his use of cell 72. In another description of the Mark I by Richard Bloch, the "register" is said to "permit the choice of one function if the value of the independent variable is less than a given quantity."¹⁸ But it is not clear if Bloch meant that the computer could turn to a completely different sequence of operations automatically depending on the value in register 72.

Given the way that the sequence of operations was fed into the machine-by a long strip of punched paper tape-it is clear that full conditional branching capability could not have been built into it without some difficulty. There was only one paper tape reader on the Mark I to read operations (three others read tapes containing data). The readers ran the tapes in only one direction. Branching to a different sequence would have required the tape to skip over instructions without executing them. It probably would have also required that the tape be able to back up and repeat a group of instructions in a loop. There would have to be a way for the tape to sense both where it was in a sequence and where the next part of the sequence was located-two pieces of information not part of the Mark I's repertoire. In short, coding instructions by a single continuous strip of tape does not lend itself well to conditional branching. When the Mark I was fitted with that capability after the war, it was done by adding a completely separate tape reader, on which were mounted coding tapes that were repeatedly executed.

Aiken wanted a machine that could evaluate long sequences of operations in which only the argument is changed each time by a small increment. For that work there is less need for flexible branching. Even today many computer programs do little more choosing of their operations besides stopping the machine when the sequence is finished.

At least one of Babbage's writings on his proposed Analytical Engine mentions conditional branching capability. The Analytical Engine was to be capable of sensing when a computed value exceeded a certain tolerance, after which the machine would advance or back up to another part of the instruction sequence (delivered to the Engine by special "operation cards," not by a tape).¹⁹

In 1841 Ada Augusta, Countess of Lovelace, a daughter of Lord Byron and a gifted mathematician, learned of Babbage's computer and quickly mastered its operating principles. Two years later she translated into English a description of the Engine written by an Italian named L. F. Menabrea. To that translation she added a long set of notes, longer than the original description itself, in which she discussed the importance of the machine's ability to choose its own course of computations depending on what it had just computed.²⁰ In particular, she stressed the ability of the Analytical Engine to reverse its operation cards and repeat a loop of operations again and again, until a certain limit was met-precisely the ability added to the Mark I and to the Z4 after the Second World War. Countess Lovelace's notes on Menabrea's description of the Analytical Engine stand as one of the first thorough studies of the nature and power of digital computers, written a hundred years before any working computer existed.

Reckoners, ASCC, page 0057

Aiken was familiar with Babbage's writings, although he may not have been aware of Ada Augusta's commentary on the Analytical Engine. But in any case Aiken did not feel that a full branching capability was a necessary part of his Sequence Controlled Calculator.

The Mark I was built with the technology of the 1930's business machines industry, but that industry was by no means a static one. Research was constantly going on at the Endicott plant, and no doubt the Mark I benefited from that. The accumulators were based on the accumulators used in standard IBM equipment. Other components of the Mark I were taken directly from IBM's product line, modified only to the extent that they had to be in order to be coupled to the rest of the machine. Card readers, card punches, and electric typewriters could be plugged into the machine at various places. The multiplier unit of the machine computed the partial products directly, one digit at a time, and was based on the ingenious design of the IBM Type 601 multiplier first marketed in 1933.

Other parts of the computer were especially designed for it. The tape readers, for example, supplied numbers or instructions by sensing the presence of holes punched into twenty-four columns of stiff paper tape. If the tape was to supply a number, each digit was coded into a group of four holes: four consecutive lines of tape for each digit, by twenty-four columns for the full twenty-three-digit number plus sign. The four lines were punched as follows for the ten decimal digits:^2l
Decimal Digits-Up to 24 Columns 0 1 2 3 4 5 6 7 8 9 Line # ------------------------------- 4 0 0 0 0 1 0 0 1 0 1 v direction of tape movement [down] 3 0 0 0 1 0 0 1 0 1 0 2 0 0 1 0 0 1 0 0 1 1 1 = hole in tape; 0 = no hole 1 0 1 0 0 0 1 1 1 0 0
The machine read the bottom line first, twenty-four columns across.²²

If the tape was to supply an instruction, a different coding scheme was used; it will be described later. The readers themselves were physically identical to one another despite their being used for different purposes. It is conceivable that the Mark I's designers could have recognized that instructions and data in a computer are fundamentally equivalent to one another. That is of course the essence of the stored program principle; it will be discussed at greater length in Chapter 6. But there is no mention of that concept in any contemporary descriptions of the Mark I. In later years, as the stored program principle became more widespread, Aiken was reluctant to acknowledge its advantages for computer design.²³

Reckoners, ASCC, page 0058

In addition to the instruction and the value tape readers, the Mark I also had a tape reader that read in values of functions for selected arguments. Those values could be connected to a device called an Interpolator, which could calculate the value of the function for any arguments in between the values punched into the tape, using familiar methods of interpolation.²⁴ In this way the Mark I could supply--or generate-tables of the most common logarithmic and trigonometric functions, and their inverses, as needed in more advanced calculations.

The physical layout of the computer was determined by the common driveshaft that synchronized the accumulators. Like a 19th century New England textile mill, all the components of the Mark I were aligned on a common axis to be driven by the rotating shaft. That layout ensured a precise synchronization in a straightforward way. So the machine was long and narrow: fifty-one feet long, eight feet tall, and only two feet deep. Photographs of the Mark I always show it polished and neat, occupying a back wall of an equally well-polished room at Harvard.

Finally it must be said that the Mark I had a distinctive sound unlike that of any modern computer. It did its computing by electromechanical relays, not by invisible and silent electrons in a microscopic silicon chip. There was no mistaking when the Mark I was running, although it did not make a deafening clatter. It sounded rather more, as one observer put it, "like a roomful of ladies knitting.²⁵

Table 3.1 summarizes the specifications of the Mark I in 1945.
Table 3.1 THE IBM ASCC (HARVARD MARK I)

Inventors: Howard Aiken, C. D. Lake, F. E. Hamilton, B. M. Durfee.
Place: Endicott, New York; moved to Cruft Laboratory, Harvard University; then to the Harvard Computation Laboratory.
Dates: Proposed 1937; construction begun 1939; completed January, 1943; placed in operation spring, 1944; dedicated August 7, 1944. In use until 1959.
Cost: $300,000-$500,000, exclusive of R & D.
Technology: Electromechanical, 3,000 decimal storage wheels. 1,400 rotary dial switches, 500 miles of wire.
Size: 51' x 8' x 2'; 19 panels; weight 5 tons.
Number
Registers:
Decimal system, 23 digits plus sign (0 = + , 9 = - ); provision for half- or double-precision arithmetic; subtraction by 9's complements; parallel transfer of all numbers.
Memory: 72 accumulators; 60 constant registers (set by 10-position switches); 3 value-tape readers.
Processor: Multiplier and divider, multiplication by table look-up; all addition and subtraction done in accumulators; special circuits for log and antilog (to base 10), sine, and interpolation of functions.
Programming: 1 sequence tape reader, using two-address code: out-field, in-field, miscellaneous, other sequencing by plugboard; 1 "choice register" and 1 "check register," allowing internal logical control.
Speed: Cycle time: 300msec. (one rotation of shaft); multiplication time approx. 6 sec.
Input: 3 value-tape feeds, 2 card feeds, plugboard, switches.
Output: 1 card punch, 1 tape punch, 2 automatic typewriters.

Reckoners, ASCC, page 0059

THE MARK I IN OPERATION
How the Mark I actually solved problems may be considered separately from what it was physically made of; the latter is the machine's "anatomy," while the former is its "physiology." Although the Mark I's components were similar to those of commercial business equipment, it obviously worked in a different way. In fact, its physiology was remarkably similar to other contemporary computers, even if they had completely different physical anatomies.

A paper tape, called the sequence tape, supplied the instructions that commanded the computer. This tape had twenty-four channels across its width-the same as one line of a number tape. But unlike the number tape, a complete program step could be coded into one line of tape (recall that a number tape needed four lines to code a full twenty-three-digit number). The twenty-four channels were divided into three groups of eight channels each. The first field specified from which part of the machine a number was to be taken (the "out-field"), the second where a number would go (the "in-field"), and the third initiated an operation. Thus the Mark I was a two-address machine, but not in the same sense as the term is used today. The operation specified by the code in the last eight channels did not always specify an arithmetic operation to be performed on the numbers given in the two preceding fields. Most of the out-and in-codes referred to numbers in the accumulators; since those devices automatically added quantities introduced into them, there was no need to give an "add" command in the operation field to perform that most basic of the computer's operations. The operation field would have to be punched with the command for the machine to advance to the next line of coding, however; this was done by punching a hole in the seventh place (from the right) of the op-field.

So the operation, "Take the contents of Unit 5, add it to the contents of Unit 6, and go on to the next instruction," would be coded as follows:
out-field in-field misc. or op-field _ _ _ _ _ 0 _ 0 _ _ _ _ _ 0 0 _ _0_ _ _ _ _ _ _ 8 7 6 5 4 3 2 1 8 7 6 5 4 3 2 1 8 7 6 5 4 3 2 1
Holes punched in columns three and one indicate the fifth accumulator; holes punched in columns three and two indicate the sixth.²⁶ Note how this coding is different from the coding of the number tapes. The eight columns for the in- and out-fields were more than enough to address the seventy-two accumulators, sixty constant registers, and other devices.

Reckoners, ASCC, page 0060

For multiplication, the third field functioned as a true operation-code field, although multiplication was not done in a single step. First two steps loaded the numbers to be multiplied from their locations (given in the out-field of two successive lines of coding) into the multiplier unit of the machine (its code given in the in-field of the two lines). After the numbers were loaded, a command was given in the op-field to multiply, with the in- and out-fields left blank. The next line of coding gave the address of a special register designed to handle up to the forty-six digits of the product.

All in all, then, it required at least four lines of coding to perform a multiplication. Depending on the length of the numbers themselves, it took from ten to twenty machine cycles to perform the operation. Thus the maximum multiplication time was 20 x 300msec., or about 6 seconds.²⁷

If the sequence did not immediately require that product, the programmer could specify other operations on the lines of coding between the command to multiply and the command to store the product. That was, in fact, often done. So although Aiken always emphasized the sequential nature of computations in his machine, the Mark I was capable of a lot of parallel computation as well-a consequence of the dual storage and addition capabilities of the seventy-two accumulators.

Interpolation, consulting function tables, and other related functions were handled in the same way; the function tables and constant switches were also given addresses, although of course those addresses made sense only if punched into the out-field of the tape. In the same way the output facilities such as the typewriters and card punches were given addresses that could be punched into the in-field.²⁸

The functioning of the Mark I is best illustrated by an example. The following problem is probably too simple to justify using the computer for its solution, but it is representative of the types of problems the Mark I handled. The example is taken from the Manual of Operation, p. 292:
Evaluate the polynomial
F(x) = x⁴ + 3x³ - 3x²/4 - 22x + 3
by successive multiplication, in the interval 5 <= x <= 10, with
[Delta]x = 0.01 (that is, for x = 5.00, 5.01, 5.02,...10.00).

The first step is done mentally by the programmer. That is to rewrite the above expression in such a way as to minimize the number of multiplications required:

F(x) = (((x + 3)x - 3/4)x - 22)x + 3
This so-called nested parenthetical form reduces the number of multiplications from ten to only four, including one division. Inasmuch as multiplication is a time-consuming operation, it is imperative that this form be used on any problem of appreciable size.

The next step is to initialize the computer by storing the coefficients 3, -3/4, -22, and 3 in the switch (constant) registers. Other registers that are to be used in the course of the computation have to be cleared to zero-a simple matter of coding the same address in both the in- and the out-field, plus the operation to continue (the machine automatically interpreted this command to subtract the number in the accumulator from itself, leaving zero).

Reckoners, ASCC, page 0061

Finally the starting value of the independent variable, 5.00, the ending value 10.00, and the increment 0.01 are also stored.

After coding the tape to initialize the machine, codes for the actual computation can begin. That consists of a sequence of elementary operations to evaluate the polynomial for each value of x.²⁹ Once calculated, the result is sent to an output device, the value of x is incremented by 0.01, and the sequence is run through again. When all values of x have been run, the operator would stop the machine manually by pressing a button. Appendix section (2) lists the actual 36-line coding for this problem on the Mark I, followed by that same program rewritten for a pocket calculator, using the same flow of data and instructions as the original.
ERROR CHECKING AND ACCURACY
Assuming the computer has successfully run through the sequence of calculations and has printed out the successive values of x and f(x), the programmer now faces the question of whether or not those results are accurate. The Mark I was an enormously complicated device, containing three-quarters of a million individual parts. Even a simple program like the one just listed would exercise many of those parts, and they all had to function correctly if the answers were to be correct. Actually there are several different ways that errors can occur, and for each a separate treatment may be required. In his analysis of the reliability and accuracy of the Mark I, Aiken recognized four different types of errors:

Errors inherent in the mathematical formulas themselves; the equations yield only an approximation of the phenomena they describe.
Round-off errors caused by a repetition of the four basic operations of arithmetic to only a finite decimal precision (23 digits on the Mark 1).
Mistakes made by human operators: pressing the wrong buttons, setting the constant registers improperly, etc.
Errors resulting from a mechanical or electrical failure within the calculator itself.³⁰

The first type of error is part of all mathematics, whether or not one is using a computer. It was a problem that computer users faced, but then so so did every other mathematician. The other sources of error are more directly consequences of using a computer, although to a limited extent they appear even when simpler mathematical instruments such as slide rules, planimeters, or desk calculators are used. In 1944 there was no general agreement on what would be the best way to detect and minimize these errors, and so the pioneers in computing each tried a number of different approaches.

Reckoners, ASCC, page 0062

Errors of the second kind, round-off errors, are inherent in any physical process that must necessarily handle numbers of a finite length. Aiken sought to minimize these errors by providing the Mark I with an extraordinarily long word length of twenty-three digits; yet there were times when he felt that even that was not enough, and he resorted to a doubling up on accumulators to get forty-six digits. Later generations of computer designers would find ways of minimizing round-off errors while carrying fewer digits in the machine's registers-a careful analysis of the problem beforehand often would reveal just how many digits were needed to give the desired accuracy, and in many cases that proved to be far fewer than twenty-three decimal digits.

Human errors of programming, setting switches, feeding stacks of cards, and the like are much more difficult to detect the person who makes the error often repeats it when he goes over his work again. By careful attention to details, double-checking by another person, and mechanical safeguards built into the machine they may be kept to a minimum. One obvious test is to run the program as set up with data that were known to give a certain answer beforehand; if the machine does in fact deliver that answer, then it is safe to say that the operation sequence was coded onto the tape correctly (this test does not always work, of course, but it is good enough when combined with other checks). In all of those approaches, Aiken and his staff were exploring unknown territory in what would become an important branch of modern computer science.

The last type of error, due to machine malfunctions, was also difficult to detect and prevent. A machine as complex as the Mark I had thousands of places where something could go wrong at every step of a computation. Aiken stressed one approach to that problem-an approach which curiously reveals his knowledge of the history of computing and his sense of his own place in that history.

The approach was to repeat the computation, using a subset of the input data, but not using the same formulas as before. If the machine yielded the same results as before while using different registers, accumulators, switches, and tape units, then it was safe to say that the original computations were correct for all their input values. If they did not agree, then further calculations could localize and evenutally isolate the defective components. (A good computer programmer is like Sherlock Holmes-when a program does not work the programmer has to be able to piece together bits of strange and seemingly incomprehensible evidence to find the culprit.)

The alternate method Aiken chose to evaluate polynomials was that of finite differences- the same method that started Charles Babbage on his long, frustrating road to computers in 1822. So Aiken not only acknowledged Babbage as the inspiration for his plans to build a sequence controlled calculator, but he also incorporated some of Babbage's very methods into his machine as a way to check its reliability.³¹

The link between Babbage and the modern computer age is a complex one. Other computer pioneers from the 1935-1945 era knew of Babbage: Zuse in Germany, Vannevar Bush at MIT, perhaps a few others. But Aiken, and probably only he, consciously saw his own role as one of picking up where Babbage had left off a century before.³² In his published descriptions of the Mark 1, Aiken always gave generous credit to Babbage as the true pioneer in computing.

Reckoners, ASCC, page 0063

Most accounts of the history of the computer mention Babbage's Analytical Engine as the machine that began the computer age. That is because in it one finds all the functions that a true computing system requires: program control, memory, arithmetic unit, and input/output facilities. The Analytical Engine was furthermore consciously designed to be a general-purpose computer, and that, too, is a central feature of today's computers. But Babbage came to the idea of building the Analytical Engine after first building a test model, then planning a full-scale model, of a more modest Difference Engine. (The test model of the Difference Engine was the only machine that he ever finished.)

The Difference Engine was to have computed the values of polynomials by summing up finite differences: by mechanizing only the operation of addition (obviously much easier than mechanizing all the arithmetic operations). The method of finite differences could nonetheless evaluate precisely the same kinds of functions that the Mark I was planned to evaluate. Thus it was a good way to check the Mark I's circuits, as the additions could be programmed in any of the seventy-two accumulators, checking the answers yielded by the multiplier, divider, and other more complex parts of the machine during a regular run of a program. Aiken conceived of the Mark I as the direct successor of the Analytical Engine, and the Mark I was a general-purpose computer. But the spirit of the Difference Engine lived in it as well.
THE METHOD OF FINITE DIFFERENCES
Values of higher-order polynomials like the one given above may be evaluated using only simple additions, once certain initial values have been calculated. That was the secret of the Difference Engine: it could be mechanically simple, yet mathematically sophisticated, by an ingenious linking of its wheels to one another.

The following table lists the values of the function given above:

F(x) = x4 + 3x3 - 3x2/4 - 22x + 3
for the integer values of x from 5 to 10:

x F(x) 1st diff. 2nd diff. 3rd diff. 4th diff. 5th diff.
5 874.25
. . 913.75
6 .1788.00 . 540.5
. . 1454.25 . 174
7 3242.25 . 714.5 . 24
. . 2168.75 . 198 . 0
8 5411.00 . . 912.5 . 24
. . 3081.25 . 222
9 8492.25 . . 1134.5
. . 4215.75
10 12708.00

Reckoners, ASCC, page 0064

The numbers in the columns to the right of F(x) are obtained by subtracting the two adjacent values in the column immediately to the left (for example, the first entry in the column labeled "1 st diff.," 913.75, is the difference between F(6) and F(5), the two numbers immediately to its left). The first entry in the column labeled "2nd diff." is the difference of the first two entries in the first-difference column, and so on.

Note that the fifth difference is zero, and that the fourth difference is a constant value (24). For any polynomial of the nth degree (the degree is the highest exponent that appears in the expression), the nth difference will be constant. (It is in fact

n!([delta]x)ⁿa_n
Where n! is the product n(n-1) (n-2) (n-3). . .(1), Ax is the increment value of x, and a_n is the coefficient of the highest exponent of x. In the above example the increment of x is 1, the coefficient is 1, and the degree is 4, so the fourth difference is 4!, or 24.)

So by calculating the constant nth difference, plus a few initial values of the intermediate differences (that would have to be done by hand), one can construct a table like the one above for more complex equations, using only the operation of addition. Furthermore, those polynomials could approximate, as accurately as one wished, any equations that one encountered in descriptions of real-world phenomena-including the far more difficult and refractory transcendental functions such as exponentials, logarithms, trigonometric functions, as well as the more exotic Bessel and elliptic functions that would be the grist for the Mark I's mill throughout its lifetime.

Hence Babbage's Difference Engine would have been a powerful mathematical tool had it been completed. Even though it was limited to ordinary polynomials, given enough levels of differences it could have approximated just about any function a mathematician would have required-accurately, tirelessly, mechanically. In Aiken's own words: "Thus the calculus of finite differences has become the bridge between mathematical analysis and numerical computation."³³

In 1864, long after Babbage had given up hope of ever completing either of his computing engines, he wrote:
Half a century may probably elapse before any one without those aids which I leave behind me, will attempt so unpromising a task. If, unwarned by my example, any man shall undertake and shall succeed in really constructing an engine embodying in itself the whole of the executive department of mathematical analysis upon different principles or by simpler mechanical means, I have no fear of leaving my reputation in his charge, for he alone will be able to appreciate the nature of my efforts and the value of their results.³⁴
Howard Aiken chose that quotation to introduce the Manual of Operation of the Mark I.

Reckoners, ASCC, page 0065

The Mark I evaluated functions directly. The method of finite differences was used only as a check since it used different parts of the machine and was coded in a different way without any multiplications. Results of the two methods were compared in register 72, using its comparison feature: the machine stopped if the two answers did not agree.³⁵ Computations were checked frequently: as often as every twenty minutes to ensure that the machine was not spewing out volumes of nonsense. Besides using that check, problems were often recorded and run again using the same direct evaluation method, but using different parts of the machine. In all, the checking of the machine for errors was an important, time-consuming part of the work of the Harvard Computation Laboratory.

At its public unveiling, the Mark I was hailed as "Babbage's dream come true." Aiken succeeded in building the Analytical Engine that Babbage failed to build. But there were important differences between the two. Their anatomies were different: the Analytical Engine was to have been powered by steam, the Mark I was driven by electricity. Numbers in the Mark I were transmitted by wire, not by mechanical linkages. But there were also more fundamental differences. Their physiologies were different as well; had Babbage completed his machine it would have been programmed differently (more like modern computers than like the Mark I, actually). That is the result of the Mark I's arithmetic having been spread out through its memory units.³⁶

Howard Aiken probably did not perceive those differences, or if he did, he did not think they were important. It is not clear exactly how much Aiken really drew from his knowledge of Babbage besides the general idea. His 1937 proposal said that the Analytical Engine was to have evaluated algebraic formulas "by the method of finite differences," which was not true. Others have pointed out how, if Aiken had been familiar with Babbage's writings, and especially with Ada Augusta's comments on his work, he would certainly have recognized the importance of fitting his machine out with full conditional branching capabilities - something he did not do until after the Second World War when he learned of other computers that did have them.³⁷

But the spirit of Babbage lived in the clicking relays of the Mark 1. By 1959, when the machine was dismantled, those relays seemed as quaint and old-fashioned as Babbage's "store," "mill," and Jacquard control. Babbage once remarked that he would gladly give up the rest of his life for the opportunity to live a few days in the distant future.³⁸ Had he been granted his wish and come back to earth in the 1980's, when executives are stuffing computers into their attache cases while their children are stuffing quarters into computer games at the local mall, he might be bewildered by it all. But if he could have returned in 1944 to the Harvard Computation Laboratory, where he could have seen the Automatic Sequence Controlled Calculator gobble up paper tape and whack out long tables of Bessel functions on a typewriter, he would have felt right at home.

Reckoners, ASCC, page 0066

HOW THE MARK I WAS USED
The various magazine and newspaper articles which announced the dedication of the Automatic Sequence Controlled Calculator in 1944 accurately described its size, weight, storage capacity, and other physical specifications. But they were necessarily vague as to the intended use for the computer. Most said only that it would be used for classified problems by the Navy. Later accounts said that the Navy used it "for ballistics and ship design. . . also... some problems in lens design."³⁹ No doubt the ballistics work included the preparation of firing tables. The wartime need for those tables was a major force behind the development of computers in the United States. It was the sole purpose for which ENIAC was built. One other problem for which the Mark I was used was "a highly secret, mathematical simulation of the first atomic bomb." That calculation is still classified, but it might have been a calculation of the bomb's blast effects.⁴⁰

But the main use for the computer was for the preparation and printing of tables of mathematical functions-the same use Babbage intended for his Difference Engine. Time magazine devoted a cover story in 1950 to the new computers; in that story the Mark I had acquired an affectionate nickname from its programmers-"Bessie"-because she computed Bessel functions.⁴¹ By 1950 the urgent wartime problems were gone; other military work was better done on the newer and faster computers at Harvard and elsewhere. "Bessie" settled into a daily routine of computing and printing tables of the various Bessel functions, and that would remain her work until she was dismantled in 1959.
BESSEL FUNCTIONS
It was the desire to solve differential equations that started Howard Aiken on his path to the design of an automatic computer. Such equations describe physical phenomena in terms of a rate of change of a quantity that varies with time: hence the name "differential." One particular differential equation arises frequently in the study of vibration and periodic motion, and it involves not only rates of change but also second derivatives, that is, rates of rates of change. This equation takes the form:

x²(d²yldx) + x(dyldx) + y(x² - n²) = 0
There are two families of solutions to this equation (since it contains a second order derivative), and these are usually called solutions of the first and second "kinds." For each kind there are many different solutions depending on the value of the parameter n, which is usually a small positive integer but in fact may take on any positive real value.⁴²

Besides the two basic families of solutions, there are also functions that resemble a combination of the solutions of the first and second kinds. These are sometimes called Hankel Functions of Order N, and I mention them because the first tables that the Mark I computed were of those functions.⁴³ There are also classes of solutions defined for complex values of the independent variable, and finally, integrals of all the various Bessel functions of the various kinds.

Reckoners, ASCC, page 0067

It was the job of the numerical analyst or engineer to determine which of the above functions (if any) was applicable to a particular problem at hand; appropriate values of n and x also had to be selected. That was often the most difficult part of the analysis of a physical problem. But there still remained the problem of evaluating the Bessel function itself. The Bessel functions resemble the trigonometric functions in that they are periodic and often regularly pass through the zero value (the so-called zeros of the Bessel functions). But there is no easy way to evaluate them. The analyst had to select a polynomial approximation that fit the Bessel function closely enough for the interval he or she was interested in-using techniques already well known in Babbage's time. Obviously it would be advantageous if the engineer or mathematician could consult a table of those values rather than compute them every time they were needed. It was the task of the Mark I to compute (using appropriate polynomial approximations) and print tables of the various kinds of Bessel functions for a wide range of arguments. The many different kinds of functions and the range over which their values were tabulated ensured that the Mark I would be busy for many years-even after other more advanced computers had long made its design and technology obsolete. The computations themselves were long and involved, but they suited the abilities of the Mark I well, and they were not hindered by the machine's limitations.

Bessel functions are used throughout the sciences and engineering. A typical application might be the vibration of a plate that is fixed at its perimeter (like a drum-head). The vibration at any point is a function of the elasticity of the material, its tension, and the distance of that point from the fixed perimeter. Another common application is the analysis of radio transmissions, especially FM signals, in which the regular vibration of the carrier wave is modulated by a signal that carries the voice or other information. Even the structure of the DNA molecule, consisting of a periodic repetition of a basic chemical structure, was unraveled with the help of Bessel functions.⁴⁴

That was how the Mark I was used. In the years following the war, Harvard University Press brought out a series of those tables, and they are available in libraries throughout the world as the Annals of the Harvard Computation Laboratory, volumes 2 through 36. The first of them, the tables of Hankel Functions of Order One-Third, was coded on the machine in August, 1944, and was run successfully that fall and winter. The entire set of tables contained over 70,000 eighteen-digit quantities and took the equivalent of forty-five days to be computed. Because that work had to be sandwiched in between the other war-related computations, the Harvard staff could not compute the tables in a long continuous run, and so they had to retype the numbers by hand before they could be published.

Reckoners, ASCC, page 0068

Subsequent tables were printed directly from the output of the Mark I's output devices, which greatly reduced errors in copying and typing long strings of digits. (Such errors were frequent in any tables set by hand-Babbage saw the elimination of that step as a decisive advantage of his Difference Engine).⁴⁵ The tables themselves were computed by evaluating suitable polynomial approximations for given intervals, and then checked by alternate methods of direct evaluation (not, however, by the method of finite differences).

In his review of the speed and power of the machine, L. J. Comrie observed that though the tables were useful and their evaluation took a lot of effort, the work could nevertheless have been done by teams of human beings equipped with desk calculators. He asked, "Does the calculator open up new fields in mathematical and numerical analysis?"⁴⁶ That is hard to say: it did do more than compute tables. But for the most part it performed yeoman service for mathematicians and engineers. It never did anything glamorous like crack codes or design secret weapons, but the Mark I represented a breakthrough in computing nonetheless. The tables themselves were well-used, although by 1959 other tables of the same functions were also available. Sales of the volumes brought in money for the Computation Lab, money that financed the construction of other computers at Harvard.

Whatever else it did, it spelled the end of the era of computing tables by hand. Even today, when computing power is cheap and widespread, there is still a need for tables of the more complex functions. After the war the National Bureau of Standards undertook a compilation of the most frequently used tables (using the Mark I's work for the Bessel Functions). The NBS's Handbook of Mathematical Functions became a staple of many a working mathematician's library. A numerical analyst today can compute the desired values f one of the simpler Bessel functions at his desk, using a pocket calculator or personal computer, but there are many times when that procedure is neither practical nor accurate enough. The computer itself has brought the field of numerical analysis to a new level, where even more tables, more accurate and more elaborate, are needed. All of that activity may be said to be part of the legacy of Howard Aiken and the Automatic Sequence Controlled Calculator.⁴⁷
POSTWAR COMPUTING AT HARVARD
The rift between Aiken and IBM that surfaced before the dedication ceremony grew after the war. It was not just the dispute over whether the ASCC was to be covered or not. Thomas Watson felt that Aiken was unwilling to share any credit for the success of the project. In 1944 IBM was not the industrial giant it is today. Aiken felt that the computer was his idea; whoever happened to build it was of little import. The Harvard Lab continued building computers under Aiken's direction-but not with IBM's help. (The Harvard machines took on the names "Mark I," "Mark Il," and so on.)⁴⁸

Aiken was never convinced that vacuum tubes would make good computer components, and so his machines continued to use relays long after much faster electronic computers were completed elsewhere. He did use tubes in the Mark IV, but only for a few units where speed was absolutely needed; everywhere else he used relays.⁴⁹ But by 1950 other pioneers were arguing that computers should use only vacuum tubes, handle numbers in binary not decimal form, and store their programs internally. On all those features Aiken swam against the stream, and he did not prevail.

Reckoners, ASCC, page 0069

Meanwhile, Watson and IBM had a bitter first taste of large-scale computing, but they were smart enough to remain involved in the new technology. They of course continued to develop and market faster punched card machines, like the 603 electronic multiplier already mentioned. One of their customers, the Northrop Aircraft Company, hooked up an improved type 604 multiplier to an IBM 402 accounting machine, and with that they had a reliable automatic calculator of modest power. IBM recognized Northrop's ingenuity and followed in 1949 by marketing their own Card Programmed Calculator based on that lashup.⁵⁰

But the CPC was not capable of fully general program control like the Mark I, although its reliability and low cost made it a very successful product. The company also went on to build a large-scale computer along the same lines as the Mark I, which they called the Selective Sequence Electronic Calculator, built in Endicott and dedicated in 1948. As the name suggests, the SSEC could branch to different sequences in its instruction set, but despite its name, it was more a relay calculator like the Mark I than a true electronic computer. It used vacuum tubes only for a central high-speed processing unit; electromechanical parts were used elsewhere. It handled numbers in the decimal system, and despite the fact that it could store (and even modify) some of the instructions in its high-speed memory, its architecture owed more to the punched card, plugboard technology than to the new ideas about stored-program computers that were current by 1948. (Nonetheless, it must be given credit as the first machine to function with a stored program capability.) The SSEC was dismantled in 1952, but it maintained IBM's foothold in large-scale computing at a critical time, and that foothold would be vital to the company's entry into the mainframe computer business a few years later. (The company marketed its first true stored-program electronic computer, the 701, in 1952.)⁵¹

The SSEC was installed in a prominent place at IBM's New York offices on 57th Street, in full view of passers-by. (When the machine needed maintenance, curtains had to be drawn to prevent the public from seeing the machine with its panels down.) Like the Mark I it was well publicized, and the SSEC gave ordinary people their first glimpse of what a real computer looked like. One little-known fact is that it alone among the early computers was available for private use, at a charge of $300 an hour. All the other machines were used primarily by the military, with only "extra" time, if there was any, allocated to civilians.⁵² IBM deserves credit for that innovation as well.

In conclusion, Aiken's work at Harvard was an impressive first step into the computer age. But it did not contribute directly to the mainstream after 1950. The fact that his laboratory was publicized meant that he became a clearinghouse for correspondence and information about computers for those who were not privy to other sources of knowledge. As a result he was always at the center of later computer activity, even though his aversion to electronics and to the stored program principle meant that his ideas had little influence.

Reckoners, ASCC, page 0070

The Computation Laboratory was perhaps his most lasting achievement. It provided a place where a new generation of students could learn about computers, and many of his students went on to become pioneers in their own right-to be sure, in ways that Aiken might not have understood. (Ken Iverson, the designer of the language APL, and Fred Brooks, who worked on the IBM 360, were two of Aiken's students.) He remained on the staff until his retirement in July, 1961, after which he did some private consulting. He died in 1973; by then his reputation as a pioneer was quite secure.

NOTES

Howard Aiken, "The Future of Automatic Computing Machinery," Elektronische Rechenanlage and Informationsverarbeitung (Darmstadt, 1956), p. 33.
William Rodgers, Think: A Biography of the Watsons and IBM (New York: Stein and Day, 1969), p. 172; "Giant New Calculator," Science News Letter, August 12, 1944, cover; August 19, 1944, p. 111; Volta Torrey, "Robot Mathematician Knows All the Answers," Popular Science Monthly, 145 (October, 1944), 86-89, 222, 226, 230.
Henry Tropp, "The Effervescent Years: A Retrospective," IEEE Spectrum, 11 (February, 1964), 70-81.
Anthony Oettinger, "Howard Aiken," Communications ACM, 5 (June, 1962), 29.
Howard Aiken, "Proposed Automatic Calculating Machine," IEEE Spectrum, 1 (August, 1964), 62-69.
Howard Aiken, "Historical Introduction," A Manual of Operation for the Automatic Sequence Controlled Calculator, Annals of the Harvard Computation Laboratory, vol. 1 (Cambridge, Mass.: Harvard, 1946), p. 8; Tropp, "Effervescent Years," pp. 72-73.
Brian Randell, The Origins of Digital Computers: Selected Papers, 2nd ed. (New York: Springer, 1973), p. 127; Rodgers, Think, pp. 166-169; Charles and Ray Eames, A Computer Perspective (Cambridge, Mass.: Harvard, 1973), pp. 114, 173.
Rodgers, Think, pp. 169-171.
Manual of Operation, preface, forward; Tropp, "Effervescent Years," p. 73; Rodgers, Think, p. 169.
Rodgers, Think, pp. 169-171.
Byron E. Phelps, "The Beginnings of Electronic Computation," Report TR 00.2259, IBM Corporation, Systems Development Division (Poughkeepsie, N.Y.: IBM, Dec. 9, 1971).
Wallace J. Eckert, Punched Card Methods in Scientific Computation (New York: Thomas J. Watson Astronomical Computing Bureau, Columbia University, 1940).
Manual of Operation, preface; Richard M. Bloch, "Mark I Calculator," Annals of the Harvard University Computation Laboratory, 16 (1947), 23-30.
"Giant New Calculator," p. 111; Thomas G. Belden and Marva R. Belden, The Lengthening Shadow: The Life of Thomas J. Watson (Boston: Little, Brown, 1962) pp. 258-261; Rodgers, Think, pp. 169-171.
Edmund C. Berkely, Giant Brains, or Machines that Think (New York: Wiley, 1949), pp. 89-93; J. H. Curtiss, "A Review of Government Requirements and Activities in the Field of Automatic Digital Computing Machinery," Theory and Techniques for Design of Electronic Digital Computers, Lectures Given at the Moore School, July -August 1946 (Philadelphia, 1947), lecture 29; Manual of Operation, p. 22; Margaret Harmon, Stretching Man's Mind (New York: Mason/Charter, 1975), p. 118.

Reckoners, ASCC, page 0071

Howard Aiken and Grace Hopper, "The Automatic Sequence Controlled Calculator I," Electrical Engineering 65 (1946), 384-391; Bloch, "Mark I Calculator," pp. 23-30.
Aiken and Hopper, p. 205; Bloch, pp. 24-25.
Bloch, pp. 24-25.
Randell, Origins, pp. 11, 187-188; Grace Hopper, "Computer Software," Computers and Their Future (Lladudno: Richard Williams, 1970), pp. 7/3-7/26; Berkeley, Giant Brains, pp. 90, 112.
Philip and Emily Morrison, eds., Charles Babbage and His Calculating Engines: Selected Writings by Charles Babbage and Others (New York: Dover, 1961), pp. 245-295.
Berkeley, Giant Brains, p. 96.
Randell, Origins, p. 216.
Manual of Operation, p. 45.
Howard Aiken and Grace Hopper, "The Automatic Sequence Controlled Calculator--II," Electrical Engineering, 65 (1946), 449-454.
Jeremy Bernstein, The Analytical Engine (New York: Random House, 1964), p. 54.
Berkeley, Giant Brains, p. 98.
Manual of Operation, pp. 32, 111-119, 296; "Mark I," Encyclopedia of Computer Science" (New York: Petrocelli/Charter, 1976), pp. 852-853.
Howard Aiken and Grace Hopper, "The Automatic Sequence Controlled Calculator III," Electrical Engineering, 65 (1946), 522-528.
Manual of Operation, p. 16.
Aiken and Hopper, "Automatic Sequence. . .-III."
Joseph 0. Harrison, Jr., "The Preparation of Programs for the Mark I Calculator," Proceedings of a Symposium on Large-Scale Calculating Machinery, Annals of the Harvard Computation Laboratory, vol. 16 (Cambridge, Mass.: Harvard, 1948), pp. 208-210.
N. Metropolis and J. Worlton, "A Trilogy on Errors in the History of Computing," Proceedings First USA-Japan Computer Conference, Tokyo, 1972, pp. 684685.
Manual of Operation, pp. 10, 296-304.
Morrison and Morrison, Charles Babbage, p. 142.
Manual of Operation, pp. 10, 296-304.
L. J. Comrie, "Babbage's Dream Come True," Nature, 158 (October 26, 1946), 567-568; Tropp, "Effervescent Years," p. 73.
Randell, Origins, pp. 187, 192; Metropolis and Worlton, "Trilogy," pp. 684-685.
Morrison and Morrison, Charles Babbage, p. xxxi.
Science News Letter, August 12, 1944, p. 11; Time, August 14, 1944, p. 72; Eames, Computer Perspective, p. 122.
"Mark I," Encyclopedia, p. 853.
Time, January 23, 1950, pp. 54-60.
M. Abramovitz and 1. Stegun, Handbook of Mathematical Functions (Washington, D.C.: National Bureau of Standards, 1964), pp. 358-494; Frank Bowman, Introduction to Bessel Functions (New York: Dover, 1958).
Published as the Annals of the Harvard Computation Laboratory, vol. 2, 1945.
Bowman, Bessel Functions, pp. 122-134; Francis Crick, "The Double Helix: A Personal View," Nature, 248 (April 26, 1974), p. 766.

Reckoners, ASCC, page 0072

The tables were reviewed in Mathematical Tables and Other Aids to Computation, 2 (1946), 176-177.
Annals of the Harvard Computation Laboratory, vol. 2, introduction; Comrie, "Babbage's Dream," p. 568; Morrison and Morrison, Charles Babbage, p. 314.
Herman H. Goldstine, The Computer from Pascal to von Newmann (Princeton: Princeton University Press, 1972), p. 17.
Rodgers, Think, p. 178; Randell, Origins, p. 188.
Oettinger, "Howard Aiken," p. 298.
John W. Sheldon and Liston Tatum, "The IBM Card-Programmed Calculator," in Randell, Origins, pp. 229-235.
Cuthbert Hurd, "Early IBM Computers: Edited Testimony," Annals of the History of Computing, 3 (1981), 168; Belden, Lengthening Shadow, pp. 258-261.
Time, January 23, 1950, p. 59.

Go Forward, Go Back, Go to Table of Contents, Go to On Line Documents, Go to Go to Antique Computer home page