Used in the Text
The following glossary gives a brief description of some of the technical
terms discussed in
the text. During the early history of computing, few of these terms had a
fixed meaning.
Some, like computer itself, changed their meanings several times from 1935
to the present.
Others, like accumulator, had well-defined meanings but various individuals
interpreted them
differently. In all cases I have attempted to provide a definition of a
term as it might have
been defined in the period from 1935 to 1945. Where this definition is at
variance with the
modern one, I give that too.
Accumulator. A mechanical or electrical device which is capable of both
storing a number
and adding another number to it. Contrast with register (q.v.), which can
store but not
add. The main difference between the two is that an accumulator's digit
elements are
linked to one another so that a carry may take place. See also counter.
Addressing. The method by which a computer stores and retrieves data from
its memory
cells. Typically each cell is given a numerical address, and appropriate
circuits direct the
computer to connect a cell with a given address to its central arithmetic
unit.
Algorithm. One of the most fundamental concepts in computing. "A finite set
of rules which
gives a sequence of operations for solving a specific type of problem,"
according to
Donald E. Knuth (The Art of Computer Programming, vol. 1 [Reading, Mass.,
1969], p.
4). A precise and unambiguous recipe which is sure to lead to an answer to
a problem.
Arithmetic. The four fundamental operations of addition, subtraction,
multiplication, and
division. Sometimes the operation of taking the square root is included.
The arithmetic
unit of a computer is usually fitted with the capability of performing only
those
operations. All other "computing" must be built up of combinations of them,
plus storing
and retrieving numbers from the memory.
Binary. Any representation of numbers or logical values by a system in
which only two
possible states are allowed. A simple switch, a two-position lever, a
relay, or a flip-flop
are all binary devices. Binary numbers are usually written as combinations
of the two
binary digits 1 and 0; binary logic is usually expressed as combinations of
true and false
values. Konrad Zuse used the letters L and O for both, and in a computer it
is common to
mix both logical and numerical values.
| Reckoners, Rev.?, page 0156
|
Calculator. A machine which manipulates primarily numerical data. Before
1935: usually a
desk-sized machine that performed the four operations of arithmetic.
1935-1945:
sometimes used synonymously with computer. Today: a computing device which
operates in the (binary coded) decimal system and which is optimized for
numerical
calculations. If such a device is programmable, the program is usually
stored in a
memory kept separate from the data memory.
Calculus. Latin word for pebble-a stone used as an aid to counting. Modern
collo-
quial meaning refers to the method of differentiating and integrating
functions, as
simultaneously discovered by Isaac Newton and G. W. Leibniz in the 17th
century.
Its general meaning (as, say, Konrad Zuse used it) is the expression of
mathematical
concepts by a system of well-defined symbols.
Compiler. A computer program whose output is another program-one which can
then
be directly executed by the circuits of the machine. Compilers allow one to
write
programs using a richer and more familiar notation than long strings of
binary digits.
Complement. The complement of a number is the difference between that
number and
10000. . . (to as many zeros as the original number has). In the decimal
system, the
complement of 354 is 1,000 - 354, or 646. (Binary numbers have corresponding
complements as well.) Computers usually subtract by adding the complement
of a
number, for example, 421 - 354 is computed as 421 + 646, or 1,067. If the
machine's registers have only three places, the "1" at the left drops out,
giving the
true difference 67. A variation of this scheme is to take the difference
between each
digit and 9, giving the so-called nines complement, instead of the "tens
complement"
just described. That has the advantage of not requiring any borrowing of
digits to
form the complement, but a 1 must be added (the so-called end-around carry)
to give
the correct answer for subtraction.
Computer. Before 1945: a person who did calculations. After 1945: a machine
capable of
the four operations of arithmetic, automatic storage and retrieval of
intermediate
results, and automatic input and output, all directed by a control unit.
The modern
definition is a machine which can manipulate symbolic information in any
combina-
tion or way one desires, and which contains an internally stored program,
which the
machine may also manipulate if desired.
Control. That part of a computer that routes numbers to and from other
sections of the
machine: memory, input/output, arithmetic. Usually directed by a program.
Counter. A physical device that represents a number and which can also add
quantities,
but only by one unit at a time. If an accumulator contains the number 354,
one can
change its contents to 454 simply by adding the digit "1" to the third
decimal place.
(Old, full-keyboard adding machines had this ability.) But for a counter to
go from
representing 354 to 454, it would have to go through all the states in
between: 354,
355, 356, . . . , 452, 453, 454. An automobile odometer is a counter: it
counts the
miles one at a time (unless someone tampers with it). Modern computers have
at least
one counter that steps through the program stored in successive memory
locations. It
normally increments itself by one unit at each program cycle, but there are
provisions
to have it make longer jumps as well. A much older definition is a table
where
business transactions were carried out with the help of pebbles, an abacus,
or a
counting board. Hence the phrases "over the counter transactions," and the
like.
Data. Latin "things which are given" (singular datum). Generally, the
material put into a
computer in coded form and then acted upon by the machine. It usually
refers to
numerical inputs as opposed to the program which is also fed in.
| Reckoners, Rev.?, page 0157
|
Electromechanical. Electrical circuits in which mechanical parts do the
actual switch-
ing, as in a relay, a household light switch, push buttons, etc.
Electromechanical
calculators work just like mechanical ones, except that the power is
supplied by an
electric motor instead of by human muscles pulling a lever or turning a
crank.
Electronic. Circuits in which all switching is done by the electrons
themselves, as in a vacuum
tube or transistor. Because the mass of an electron is so small, electronic
switches are
much faster than electromechanical ones.
Floating point. Also called "scientific notation." Representing a quantity
by two numbers:
one showing the digits of the number, the other its magnitude. The second
number tells
where the decimal point is to be placed in the first number (binary point
if using base
two).
Large-scale. Does not refer to the physical size of the machinery, even
though nearly all
the early large-scale computers were also physically very big. It refers
rather to the fact
that it can solve problems whose scale would severely tax human computers.
Solving a
system of forty simultaneous equations would be such a problem; it would be
almost
impossible to solve without an automatic computer.
Memory. Any physical device which is capable of holding the representation
of a number for
later retrieval and use. A memory is said to be random-access (RAM) if the
time it
takes to get one number from it is the same as the time to get any other
number. Cyclic
or serial memories (for example, magnetic tape units) require more time to
get some
contents than others. Some memories cannot be altered once their contents
are fixed;
they are called read-only memories (ROM).
Parallel. Doing more than one thing at a time. In computing, there are two
contexts. A
parallel data structure means that when a number is manipulated in the
computer, all of
its digits are handled at once. (Once again, mechanical adding machines
work this way.)
A parallel program structure means that more than one program step is
carried out at
once (cf. the ENIAC). Contrast with serial or sequential.
Program. A list of instructions which is supplied to a computer in coded
form, and which
causes the computer to carry out an algorithm (q.v.) that will solve a
problem. Strictly
speaking, a program must be of the form that a machine can "understand" -an
algorithm
need not be. Neither may contain any ambiguities in its expression.
Programming language. The set of symbols, plus the associated rules for
combining those
symbols, with which a computer program is written. Only in that abstract
sense do
programming languages resemble human languages. A computer "understands" a
programming language when it acts the way we want it to after being
programmed in that
language.
Register. A physical device which accepts and stores data. In contrast to
an accumulator (q.v.),
when a new number is sent to a register it overwrites whatever number is
already there.
The word register also loosely applies to units in the central processor of
a computer in
which arithmetic and temporary storage are both performed.
Sequential. Doing one arithmetic operation at a time. The classic von
Neumann
architecture specifies a computer that transfers numbers in parallel but
which executes
program steps sequentially.
Serial. Handling numbers one digit at a time. Examples are the way most
humans do
arithmetic using a pencil and paper, or the way a seven-digit telephone
number is dialed
one digit at a time.
| Reckoners, Rev.?, page 0158
|
Symbolic logic. A set of symbols and rules for their manipulation, which
treat logical rather
than numeric values. The most common form of symbolic logic handles only
the two
values "true" and "false," thereby enabling it to mesh nicely with binary
arithmetic, which is also two-valued. The "logic" of a computer refers
informally to
its internal electronic circuits. Also called Boolean algebra.
Synchronous. Operation of the computer is controlled by a central clock. A
synchronous
computer works like a symphony orchestra, in which the conductor
coordinates all
the activities of the players. All actions of the computer are done with
reference to its
clock cycle. By contrast, a human being does each step in solving a problem
as soon
as he has finished the preceding step; he does not have to wait for a
specific clock
cycle. The Bell Labs Model I was an asynchronous computer, but most others
were
(and are) synchronous.
Word. A block of physical elements in which numbers or other data are
manipulated as a
group. A "word-length" of ten decimal digits means that numbers of up to
that many
digits (to a maximum value of 9,999,999,999) can be handled as a block. Some
computers have the ability to split a word in half, thereby doubling the
number of
storage cells in the computer, while halving their individual digit
capacity. Where it
is necessary to handle numbers of greater digit length than the word
length, two
adjacent cells may be joined together, for so-called double-precision.
| Reckoners, Rev.?, page 0159
|
APPENDIX
Program Listings
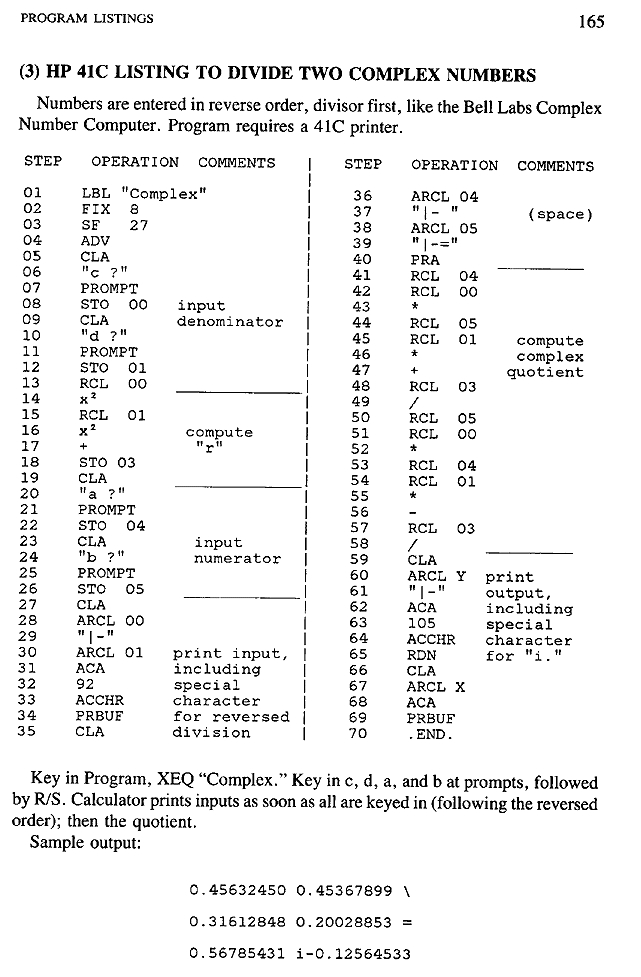
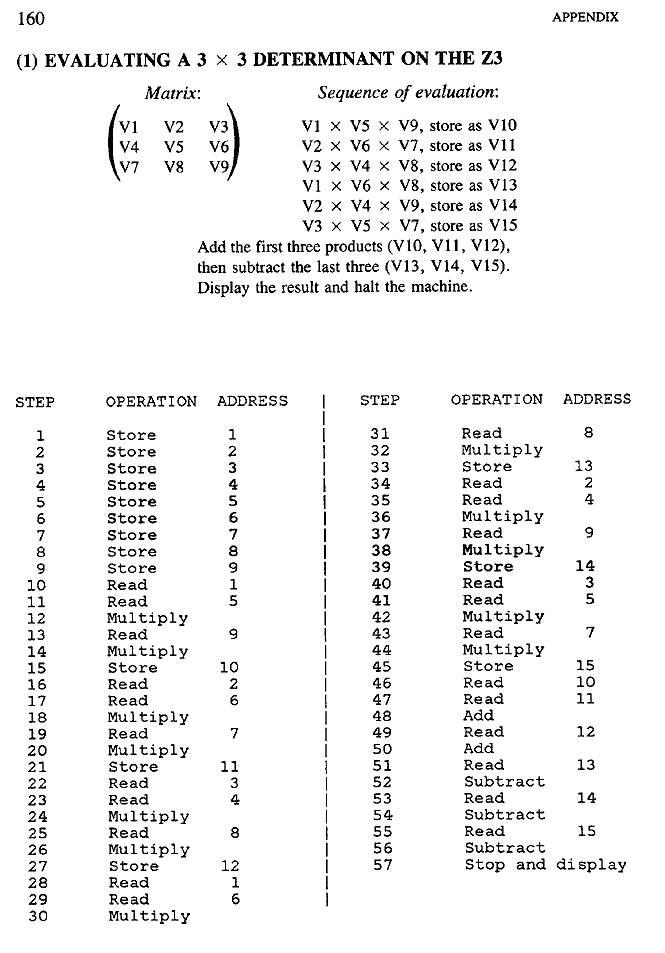
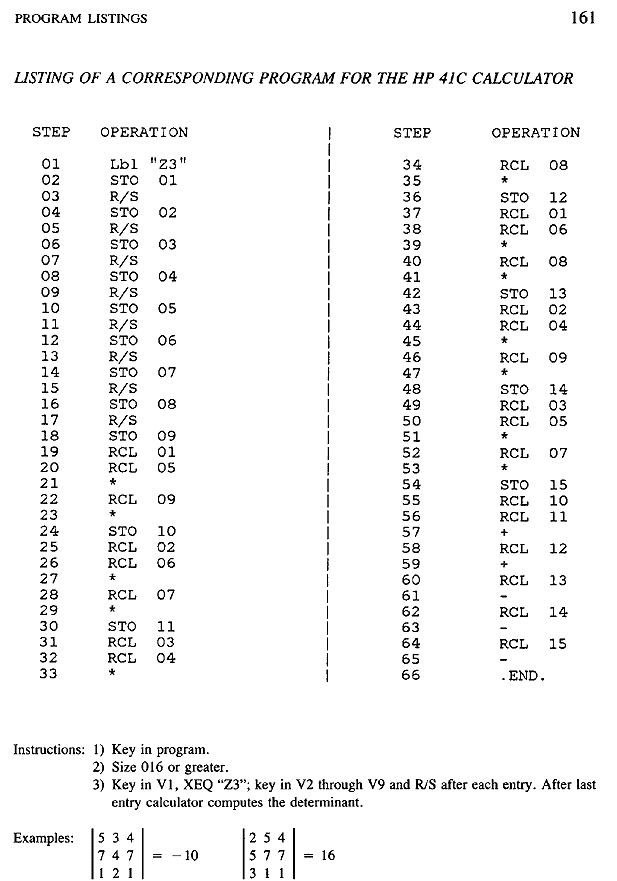
Following are listings of original program codes written for the Z3 and
ASCC. Each is then
translated into a program for an HP 41C pocket calculator. While this
calculator employs a
logic quite different from the Zuse and Aiken machines, I have written the
programs for it to
conform as closely as possible to the logical flow of the originals.
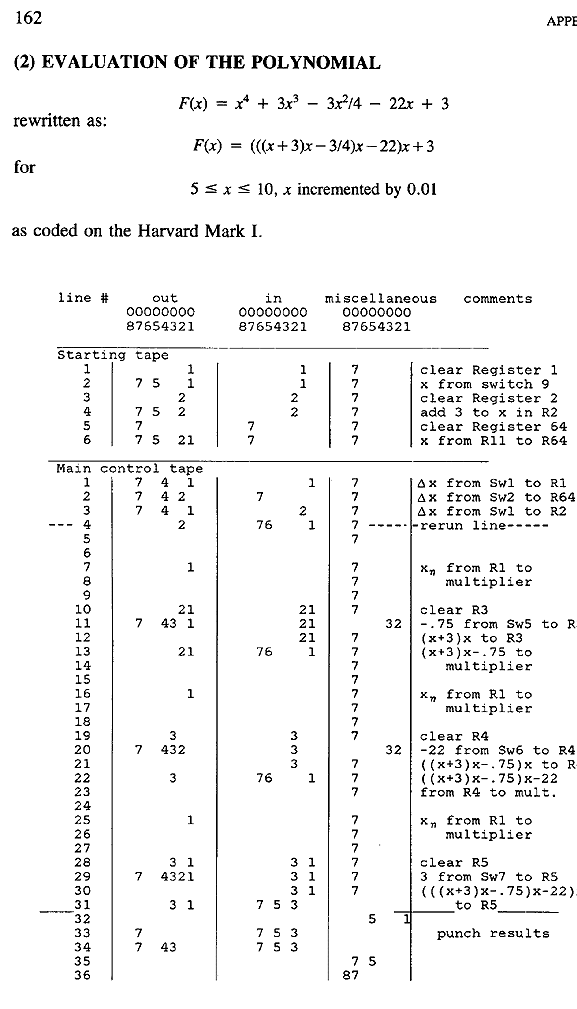
I also include a 41C program that "emulates" the operation of the Bell Labs
Model I as it
performed complex division. This program requires a printer connected to
the 41C.
| Reckoners, Rev.?, page 0160
|
| Reckoners, Rev.?, page 0161
|
| Reckoners, Rev.?, page 0162
|
| Reckoners, Rev.?, page 0163
|

| Reckoners, Rev.?, page 0164
|

| Reckoners, Rev.?, page 0165
|