THE MECHANICAL COMBINATION OF LINEAR FORMS
By D. H. LEHMER, University of California, Berkeley.
The "method of exclusion" introduced by Gauss, although a tentative method,
is still
one of the most powerful weapons for attacking many problems in the theory
of
numbers. Perhaps the most familar of such problems is the solution of the
congruence
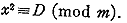 The method is also of great use in the problem of
representing a
number by a given form such as The method is also of great use in the problem of
representing a
number by a given form such as
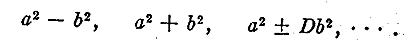 Suppose, for instance, we wish to represent a given number N as the
difference of
two squares. We may choose 5 as an "excluding number."
Let
Suppose, for instance, we wish to represent a given number N as the
difference of
two squares. We may choose 5 as an "excluding number."
Let 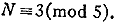 We
construct the following table We
construct the following table
 But 2 and 3 are non-residues of 5 so that the cases d=0, 1, and 4 (mod 5)
are excluded. We have then a =5n+2, 3. Other small prime moduli maybe used as
excluding numbers with the result that a is restricted to (p ± 1)/2 values
modulo p. The problem that now presents itself is the combination of the linear forms
thus obtained. If the range of d is large, it is necessary to use many excluding
numbers and the labor of combining directly these linear forms is prohibitive.
But 2 and 3 are non-residues of 5 so that the cases d=0, 1, and 4 (mod 5)
are excluded. We have then a =5n+2, 3. Other small prime moduli maybe used as
excluding numbers with the result that a is restricted to (p ± 1)/2 values
modulo p. The problem that now presents itself is the combination of the linear forms
thus obtained. If the range of d is large, it is necessary to use many excluding
numbers and the labor of combining directly these linear forms is prohibitive.
A graphical method has been suggested1 to solve this difficulty in which
use is made of a table ruled in squares, each cell representing a possible value of a.
"Movable strips" are made, the length of each being some excluding number p, and on
which impossible
Lehmer, Chain Prime ..., starting page 02
Click here for GIF version of this page
|
values of a modulo p are indicated by crosses.
These strips are moved down the columns of the table and
the cells adjacent to the crosses on the strip are then ruled out. As many
strips as are necessary are computed and applied until the number of empty
cells is reasonably small for actual trial.
But even this method has certain disadvantages. In the first place it
requires very close attention and much care. Also the strips are short in
comparison with the length of the table and have to be shifted frequently,
which is a possible source of error. Moreover the method makes it necessary
to fix the limit of the table before commencing the work, so that the whole
range must be entirely covered before any definite information can be obtained.
These difficulties are overcome by a machine constructed by the writer
for the combination of linear forms. It is the object of this paper to give
a brief description of the machine and to exhibit some of the results obtained
by it.
Here instead of strips we have chains. The number of links in each chain
is a convenient multiple of some small prime. In fact the chain lengths are:
64, 27, 25, 49, 22, 26, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, and
67. Each
chain hangs in a loop from a sprocket having 10 teeth. All the 19 sprockets
are fixed rigidly to a single shaft driven by a motor. The possible values
modulo p are indicated by small pins fastened to the appropriate links of
the chain (the zero link being indicated by red paint.) Whenever a link
provided with a pin arrives at the top of the shaft a small spring with a
tungsten point is lifted by the projecting pin. This breaks for the moment
the electric contact between the spring and a brass bar running parallel to
the shaft. By means of a relay in the circuit, the motor is shut off and the
machine stops itself. When several chains are provided with springs the
machine will not stop unless all the springs are lifted, so that every time
the
machine stops it means that a number satisfying all the imposed conditions
has appeared. This number can be read directly by means of a revolution
counter
connected to the shaft. The shaft revolves 300 r. p. m. so that the machine
canvasses 3000 numbers per minute. When all chains are provided with
springs a "solution" occurs once in several hours during which time the
machine runs without any attention.
The use of the machine is best explained by means of examples. Let us
first consider the representation of
N = (1020 + 1)/(104 + 1) = 9999000099990001
= a2 - b2
as the difference of two squares. A representation besides
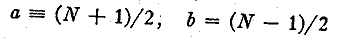
Lehmer, Chain Prime ..., starting page 03
Click here for GIF version of this page
|
is possible since N has been shown to be the product of two primes.2 The
factors of N are of the
form 40n+1. The expansion of the square root of N in a regular continued
fraction seems to
indicate that, although 21 is a residue of N, 3 and 7 are both
non-residues. The assumption that 3 is
a non-residue gives the following form for the factors of N:

where W is the limit to which the number has been searched for factors. In
this case3 W =120,000 so that a has the range
99995000 < a < 41662560416 with 13888 < k < 5786466.
Now let x=k-13888 so that 0 < x < 5772578. Then (4) gives
(5) a = 7200(x + 13888) + 7001 = 7200x + 100000601,
so that a is restricted to one case in 7200.
Lehmer, Chain Prime ..., starting page 04
Click here for GIF version of this page
|
We proceed now to exclude x with small prime moduli. Let us take for
example the
excluding number 11. We have from (5)
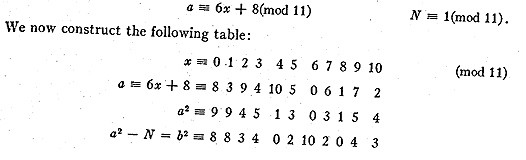
Excluding those values of x which correspond to non-residues in the last
line, we get the
following linear forms for x modulo 11:
x = 11n + 2, 3, 4, 8, 9, 10.
Other excluding numbers may be dealt with in like manner.
Kraitchik4 has given tables of the possible values of a for any N and for
excluding:-
numbers =< 47. The possible values of x can easily be obtained from the
tabulated
values of a by means of the transformation

These tables have been recalculated and the errors noted are given at the
end of the
present paper. In order to serve the needs of the machine these tables have
been
extended to excluding numbers =< 67. The use of the tables is to be
preferred to the
method illustrated by the above example. The calculation is much simpler
and the results
can easily be checked by symmetry. For instance the table for 11 gives in
our case
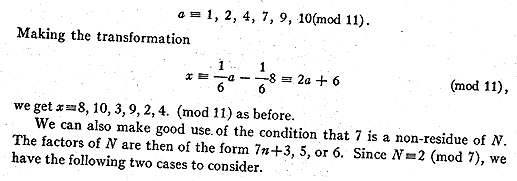
Lehmer, Chain Prime ..., starting page 05
Click here for GIF version of this page
|
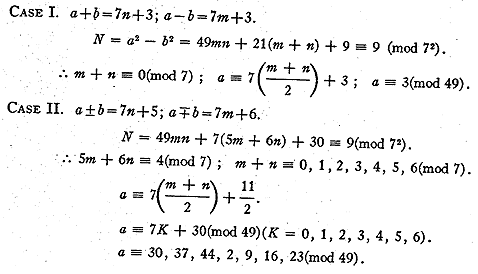
Considering both cases we have
a = 49n + 2, 3,.9, 16, 23, 30, 37, 44.
Transforming to x we get
x = 49n + 2, 9, 16, 23, 25, 30, 37, 44.
We have thus restricted x to 8 cases modulo 49 'stead of the usual 28
cases. The
result is that the machine will run longer between solutions.
Linear forms for x were thus calculated for every excluding number =< 67
and the appropriate links of each chain were supplied with pins. The machine was
then set in motion. After running about 2 hours it stopped itself at x=400453,
a = 2983262201 ; a2 - N = 8889854359815374400 = 29815858802
= b2
This gives us N = (a - b) (a +b) =1676321 X 5964848081.
If the entire range had been covered without finding the factors of N, it
would have
indicated that 3 and 7 were residues contrary to our previous assumption.
This case
could have been taken care of, without changing the position of the pins,
by simply
shifting the origin on each chain as explained later. The machine would
then have to be
set back to zero and another run made. Even if. two runs were necessary the
consideration of the quadratic character of 3 reduces the number of values
of x to 2/9.
Another example of the representation by the difference of two squares is
furnished by
N=20191210335106439, a large factorof 3111+1. Every factor of the number is of
the form 111n+1. Hence, as before, a can be restricted to one case in 1112=12321.
Also a=4n+2.
Consequently we have a=49284k+6550. The range for a is 44935627 < a <
10096101675 corresponding to W =100,000 as set by congruence tables. Hence
Lehmer, Chain Prime ..., starting page 06
Click here for GIF version of this page
|
(5) a = 49284x + 44978200 with 0 < x < 203943 .
The linear forms for x were calculated as above with the exception of those
for the excluding
numbers 3 and 37 which are not prime to the modulus 49284. The first of
these was computed
as follows. The form (5) may be written
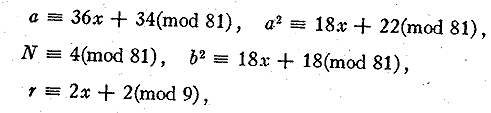
where r designates all the quadratic residues of 9, which are 0, 1, 4, 7.
Putting in these values
we obtain
x = 9n + 1, 4, 7, 8.
The linear forms for 37 were calculated in a similar way. All the linear
forms were set on the
chains and the machine, after running only 4 seconds, stopped at x=145
giving
a = 52124380 b = 26414781.
Therefore N = 20191210335106439 = 25709599 X 78539161.
If the same problem had been attacked by the "movable strip" method, the
entire range would
have been excluded before this solution was discovered.
The machine was also used to show that the other large factor of 3111+1,
namely
64326272436179833 is a prime which gives the complete factorisation
3111 + 1 = 22 X 7 X 223 X 18427 X 107671 X 25709599 X 56737873
X 78539161 X 64326272436179833.
The 5th and 7th of these primes are due to Poulet.
We consider next the representation of a number as the sum of two squares.
The
indeterminate equation x2-1721y2 = -1 has for its fundamental solution
x = 31738680901536260 y = 76506518214341.
We have then x2+1 =1721y2. Thus y is a divisor of the sum of two squares
and therefore every factor of y is the sum of two squares. We have
y = 17 X 4500383424373 = 17 X N.
We propose to represent N as the sum of two squares. Using 5 as an
excluding number we get
a=5n+2, 3. To save time we consider the two separate cases a=5x+2 and
a=5x+3. Taking the
first case we proceed to exclude values of x with all the excluding numbers
except 5. The
tables constructed for the difference of squares may be used for the sum of
squares. For an
excluding number
Lehmer, Chain Prime ..., starting page 07
Click here for GIF version of this page
|
of the form 4n+1 the entries are identical. For the case 4n+3 the entries
not tabulated
are those desired, with the exception of the pair of entries corresponding
to

The machine covered the range for the first case with but a single stop at
x = 196113, a = 980567, N - a2 = 3538871782884.
This number is not a square although it is a residue of every prime =<67.
To consider the second case, in which a=5x+3, no further calculation was
necessary.
The values of a in each case must be congruent modulo p. That is
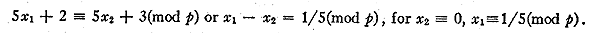
On the second start therefore, instead of setting all the chains on their
zero positions we
set them on the link corresponding to the value of 1/5 (mod p). This time
the machine
stopped only once giving
x = 157044, a = 785223, b = 1970738. Hence N = (785223)2+(1970738)2.
Since this is a unique representation, it follows that N is a prime. This
also gives us the
complete factorisation of (31738680901536260)2+1.
By separating the work into two cases, results were obtained in 2/5 of the
time required for a single run.
The machine has been used to study the following problem previously
considered by
Kraitchik,5 namely to find the least non-square which is a
quadratic
residue of all primes =< p.
Following Kraitchik, we consider 0 as a non-residue-and the number 8
instead of the
prime 2. The numbers sought belong to the forms

Letting N=24x+l we proceed to exclude values of x with moduli =>5. To
obtain the necessary linear forms we transform a table of residues by means of the
relation 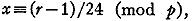 where y represents the residues of p: All the chains were
supplied with pins before starting. To start with, the chain for 5 was provided with a
spring and the machine was set in motion. The first non-square solution obtained was 241.
Then the next prime was introduced by setting on the spring of the chain for 7. The
machine was then run to the first non-square solution after which the spring for the
prime 11 was put on,
where y represents the residues of p: All the chains were
supplied with pins before starting. To start with, the chain for 5 was provided with a
spring and the machine was set in motion. The first non-square solution obtained was 241.
Then the next prime was introduced by setting on the spring of the chain for 7. The
machine was then run to the first non-square solution after which the spring for the
prime 11 was put on,
Lehmer, Chain Prime ..., starting page 08
Click here for GIF version of this page
|
etc. The squares appearing as solutions are of course squares of primes or
products
of primes >p. These squares were predicted in advance so as to avoid
unnecessary
reading of the machine. The work was carried up to p=61. The results are
summarized in the following table, which gives the least nonsquare NP that
is a residue of all primes < p.
|
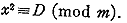 The method is also of great use in the problem of
representing a
number by a given form such as
The method is also of great use in the problem of
representing a
number by a given form such as
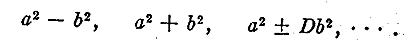
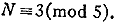 We
construct the following table
We
construct the following table

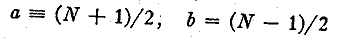



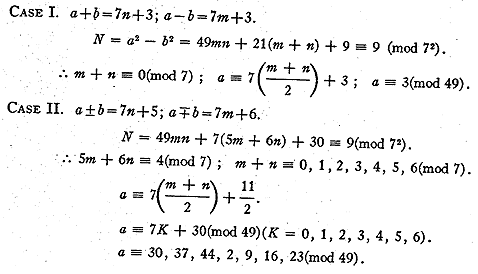
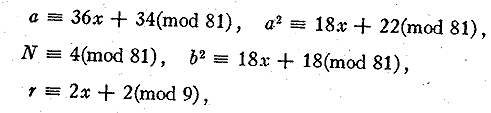

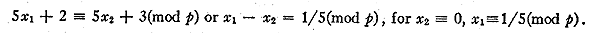

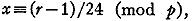 where y represents the residues of p: All the chains were
supplied with pins before starting. To start with, the chain for 5 was provided with a
spring and the machine was set in motion. The first non-square solution obtained was 241.
Then the next prime was introduced by setting on the spring of the chain for 7. The
machine was then run to the first non-square solution after which the spring for the
prime 11 was put on,
where y represents the residues of p: All the chains were
supplied with pins before starting. To start with, the chain for 5 was provided with a
spring and the machine was set in motion. The first non-square solution obtained was 241.
Then the next prime was introduced by setting on the spring of the chain for 7. The
machine was then run to the first non-square solution after which the spring for the
prime 11 was put on,
