Table of Contents
- Overview of the ABC
- Proposed Computing Group and skills
- Operator's Panel
- KeyPunch
- (decimal) KeyPunch Data Format
- Possible Binary Data Format
- Possible Pivot Comparator, non-existent
- Gaussian Elimination Algorithm, Recipe, Sequence, ...
- Improved Gaussian Elimination Need ability to compare coefficients
Much helpful info available on the Iowa State ABC website http://www.scl.ameslab.gov/ABC/ABC.html
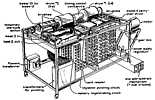 Overview drawing from http://www.scl.ameslab.gov/Projects/ABC/Progress.html |

Front view - from http://www.scl.ameslab.gov/Projects/ABC/Progress.html |
Proposed Computing Group
Operator's Panel
KeyPunch
Key Punch Data Format (decimal values, to be converted to binary)
Possible Binary Data Format
Possible Pivot Comparator, non-existent
To aid the operator with the challenge of trying to compare the absolute magnitudes of
the pivot coefficients described above, an unmentioned mechanical aid would seem useful.
The operator would place the two Binary Data Cards for the next machine processing into
two optical reader holders, and set the Comparator to focus on the line number (pivot coefficient)
of the next ABC machine processing.
These two lines of bit positions, some intact paper, some perforated by an arc,
can be made visible to the operator adjacent to each other
for easier viewing - using what ever smoke, mirrors and magnifications are necessary
to cause this effect.
Since the bit positions are likely to be 1/8 inches apart, vertically and horizontally,
some back lighting and magnification is likely to be useful.
The following major tasks could be performed by one or more people, depending ...
Operator's Panel,
Image from Charles Shorb

Top Rows
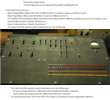
Bottom Rows
The way, (or the only "reasonable" way?) to get starting data into the ABC
is via punched "IBM Cards"
Here is an inexpensive Key Punch of the era.
(maybe an IBM Type 011 Electric Key punch?)
Photo source unknown -

Overview

Keyboard Detail
The data format for decimal input to the ABC is a repeating pattern of 5 data fields
the above format repeated 5 times,
To aid production speed and accuracy, I think we need an unmentioned operator aid.
